Пример. Пусть ![]() . Тогда
. Тогда ![]() Периодические точки являются решениями
уравнения
Периодические точки являются решениями
уравнения ![]() , поэтому они равны
, поэтому они равны 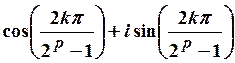 ,
где
,
где ![]() Поскольку в этих точках
Поскольку в этих точках 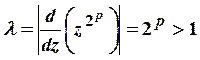 , то эти точки являются отталкивающими.
Следовательно,
, то эти точки являются отталкивающими.
Следовательно, ![]() в этом случае будет окружностью
радиуса 1, с центром в начале координат. Ясно, что
в этом случае будет окружностью
радиуса 1, с центром в начале координат. Ясно, что ![]() будет
инвариантным множеством для
будет
инвариантным множеством для ![]() и для
и для ![]() При
При ![]() значения
значения
![]() стремятся к нулю, а при
стремятся к нулю, а при ![]() - к бесконечности.
- к бесконечности.
Рассмотрим функцию ![]() , где
, где ![]() - достаточно малое комплексное число.
Тогда при малом
- достаточно малое комплексное число.
Тогда при малом ![]() значения
значения ![]() стремятся
к некоторой неподвижной точке функции
стремятся
к некоторой неподвижной точке функции ![]() , а при
больших
, а при
больших ![]() - к бесконечности. Снова множество Жюлиа
будет границей области притяжения точки
- к бесконечности. Снова множество Жюлиа
будет границей области притяжения точки ![]() .
.
Приведем текст программы для изображения множеств Жюлиа,
соответствующих различным значениям комплексного числа ![]() Преобразование
Преобразование
![]() можно записать с помощью преобразования
пар вещественных чисел
можно записать с помощью преобразования
пар вещественных чисел
![]()
![]()
Если брать различные начальные значения ![]() и применять к ним это преобразование
достаточное число раз, то в случае, когда
и применять к ним это преобразование
достаточное число раз, то в случае, когда ![]() будет
принимать большие значения, точка
будет
принимать большие значения, точка ![]() будет принадлежать
области притяжения бесконечности. Если же через достаточное число шагов она
останется внутри некоторого рассматриваемого круга, то эта точка не принадлежит
этой области. Такие точки будем окрашивать черным цветом. Точки области
притяжения бесконечности будем окрашивать оттенками серого цвета.
будет принадлежать
области притяжения бесконечности. Если же через достаточное число шагов она
останется внутри некоторого рассматриваемого круга, то эта точка не принадлежит
этой области. Такие точки будем окрашивать черным цветом. Точки области
притяжения бесконечности будем окрашивать оттенками серого цвета.
Программа.
// jul.cpp
#include <graphics.h>
#include <stdio.h>
#include <conio.h>
#include <process.h>
#include <stdlib.h>
#define MITER 8479 // количество итераций
#define a –0.11//-0.74//-1//0 // пары чисел
#define b 0.72//-0.117//0//1 //a и b
double xmin = -2, ymin = -2, xmax=2, ymax=2; // окно
int left=0, top=0, right=639, bottom=479; // область вывода
int ex(double x)
{
return left+(x-xmin)*(right-left)/(xmax-xmin);
}
int ey(double y)
{
return top+((ymax-y)*(bottom-top)/(ymax-ymin));
}
int main()
{
int gd=DETECT, gm, i;
double zx, zy, ux=a, uy=b; // параметры множества Жюлиа
double re, im, x, y, xinc, yinc, tempx, tempy;
initgraph(&gd, &gm,”..\\..\\BGI”); // инициализация графики
struct palettetype pal; // структура для палитры
getpalette(&pal); // заполнение полей структуры
for (int k=0; k<pal.size; k++)
setrgbpalette(pal.colors[k], k*4, k*4, k*4);
// палитра оттенков серого
xinc = (xmax-xmin)/640; yinc = (ymax-ymin)/480;
setfillstyle(SOLID_FILL, WHITE); // закраска экрана белым цветом
bar(0,0, getmaxx(), getmaxy());
for (re=xmin; re<xmax; re+=xinc) // пробегаются все точки
for (im=ymin; im<ymax; im+=yinc) // прямоугольника [-2,2]x[-2,2]
{
zx=re; zy = im; i=0;
do
{
tempx=zx*zx-zy*zy+ux;
tempy = 2.*zx*zy+uy; i++;
zx=tempx; zy=tempy;
} while (i<MITER&&zx*zx+zy*zy<4); // пока точка не вышла из круга
putpixel(ex(re), ey(im), 15-i%16); // закраска исходной точки
}
getch();
closegraph();
return 0;
}
Если точка не вышла из круга через 8479 шагов, то она (точнее ее исходная позиция) будет окрашена черным цветом. В противном случае она будет тем светлее, чем меньшее число шагов она находилась в круге.
Подставляя различные значения ![]() и
и ![]() получим следующие множества Жюлиа:
получим следующие множества Жюлиа:




Фракталы Ньютона. Напомним метод Ньютона
решения уравнения ![]() Рассмотрим сначала простую
задачу вычисления числа
Рассмотрим сначала простую
задачу вычисления числа ![]() , например, для
, например, для ![]() Очевидно, эта задача сводится к решению
уравнения
Очевидно, эта задача сводится к решению
уравнения ![]() , равносильного уравнению
, равносильного уравнению 
Последнее уравнение позволяет сделать вывод, что если
известно некоторое приближение ![]() , то
, то ![]() будет находится где-то между
будет находится где-то между ![]() и
и ![]()
Возьмем их среднеарифметическое и получим формулу 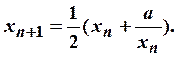 Например, для вычисления
Например, для вычисления ![]() , полагая
, полагая ![]() ,
получим значения
,
получим значения 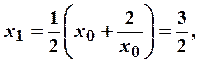
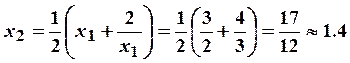 и
т.д.
и
т.д.
Можно попытаться аналогичным образом вычислить ![]() с помощью формулы
с помощью формулы 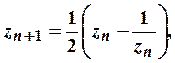 где
где
![]() принимает комплексные значения.
принимает комплексные значения.
Например, если взять ![]() , то
получим приближения:
, то
получим приближения:
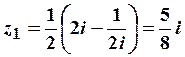 ;
;
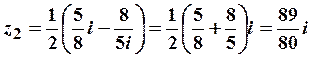 ;
;
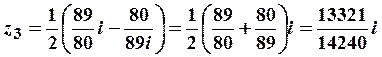
и т.д. Однако, начальное приближение
![]() , где
, где ![]() -
произвольное вещественное число, не приводит к сходящейся последовательности.
-
произвольное вещественное число, не приводит к сходящейся последовательности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.