Трехмерная машинная графика

данном учебном пособии объединяются видовое и проекционное преобразования, а проекционное преобразование производится без нормирования. Полученные таким образом координаты точки, мы будем называть координатами в пространстве изображения.

По трехмерной машинной графике рекомендуется следующая литература: /1-6, 8, 10, 14-20/.

3.1. ПАРАЛЛЕЛЬНАЯ И ЦЕНТРАЛЬНАЯ ПРОЕКЦИИ

Для изображения лежащих в трехмерном пространстве объектов координаты точек (мировые координаты) преобразуются сначала в координаты в пространстве изображения, а затем – в экранные.

Для произвольных трехмерных векторов a, b и c через (a,b,c) обозначим смешанное произведение. Скалярное произведение векторов будем обозначать через a× b, векторное – через a´b. Пусть наблюдатель находится в точке (x_V,y_V,z_V). Центральной проекцией произвольной точки (x,y,z) называется точка пересечения плоскости проекции и луча, соединяющего точку (x_V,y_V,z_V) наблюдения с точкой (x,y,z). Параллельная проекция получается из центральной, если точку наблюдения бесконечно удалить в некотором направлении.

Рассмотрим, например, шар в трехмерном пространстве. Соединяя точку наблюдения (x_V,y_V,z_V) с каждой точкой шара, мы получим круговой конус. Так как пересечение произвольной плоскости с конусом является эллипсом, то центральной проекцией шара будет эллипс, превращающийся в круг только в тех случаях, когда плоскость проекции перпендикулярна прямой, проходящей через точку наблюдения и центр шара.

Опишем формулы преобразования координат при параллельной и центральной проекции.

Параллельная проекция. Пусть задана декартова система координат (x,y,z). Рассмотрим произвольную плоскость P, проходящую через некоторую точку (x₀,y₀,z₀), радиус-вектор которой равен r₀, параллельно векторам u₁ и u₂ (рис. 16) /15/.

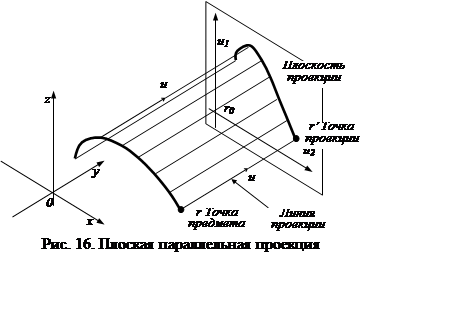Пусть u – произвольный вектор. Тогда для каждой точки r трехмерного пространства существует единственная тройка (x',y',z') вещественных чисел такая, что r=r₀+x'u₁+y'u₂+z'u.

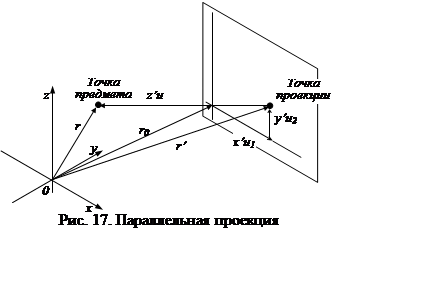
Пару чисел (x',y') мы будем называть координатами параллельной проекции точки (x,y,z) на плоскость P вдоль направления u, или параллельной проекцией на плоскость P параллельно вектору u (рис. 17) /15/.

Чтобы найти x', y' и z', умножим обе части равенства

r-r₀=x'u₁+y'u₂+z'u скалярно на векторы, выбранные таким образом, что в правой части остается лишь один ненулевой член. Умножая на u₁´ u, приходим к равенству (r-r₀,u₁,u) = y'(u₂,u₁,u). Умножая на u₂´ u, получим

(r-r₀,u₂,u) = x'(u₁,u₂,u).

Наконец, скалярное произведение на u₁´ u₂ приводит к равенству

(r–r₀,u₁,u₂) = z'(u,u₁,u₂).

Отсюда вытекает, что координаты (x',y') проекции вдоль направления u на плоскость P можно вычислить с помощью формул

x'=(r-r₀,u₂,u)/(u₁,u₂,u),

y'=-(r-r₀,u₁,u)/(u₁,u₂,u).

При применении алгоритмов удаления невидимых линий необходимо знать координату, характеризующую степень удаленности точки от плоскости P. Согласно выкладкам, эта координата равна  z'=(r-r₀,u₁,u₂)/(u₁,u₂,u).

Пример 3.1. Рассмотрим параллельную проекцию трехмерного пространства на плоскость Oyz в направлении вектора u=(1,0.7,0.7). Плоскость Oyz можно задать векторами u₁=(0,1,0), u₂=(0,0,1).

Смешанное произведение (u₁,u₂,u) равно 1. Поэтому

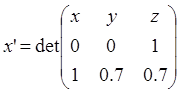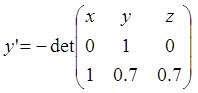,             , отсюда находим x'=-0.7x+y, y'=-0.7x+z.

Пример 3.2. Рассмотрим ортогональную проекцию на плоскость, проходящую через начало координат, заданную единичным вектором нормали n. В этом случае u=n. Вектор u₁, обычно, (например, в архитектуре или в военном деле) берут лежащим в горизонтальной плоскости Oxy. Этот вектор должен быть ортогонален вектору u, поэтому при u₁={x,h,0} выполнено соотношение x u_x+h u_y=0. Решая это уравнение получаем u₁, а затем u₂:

u₁={-u_y/sqrt(u_x²+ u_y²), u_x/sqrt(u_x²+u_y²), 0},

u₂={-u_xu_z, -u_yu_z, u_x²+u_y²}/sqrt(u_x²+u_y²).

Центральная проекция. Пусть задана плоскость с началом координат r₀ и базисными векторами u₁ и u₂ (рис. 18) /15/. Требуется изобразить на плоскости проекцию точки r=(x,y,z) из точки наблюдения r_V. Пусть (x',y') – искомые координаты. Тогда для некоторого lÎR выполнено равенство