Глава 9. Элементы гиперкомплексной динамики
Здесь мы рассмотрим квадратичное
отображение в ![]() -х мерном гиперпространстве
-х мерном гиперпространстве ![]() , исследуем свойства замыкания множества
отталкивающих точек, которое является аналогом множества Жюлиа [22]. В заключение
приведем компьютерные визуализации этого множества.
, исследуем свойства замыкания множества
отталкивающих точек, которое является аналогом множества Жюлиа [22]. В заключение
приведем компьютерные визуализации этого множества.
Далее, следуя [23], рассмотрим задачу
построение цветных паттернов (мозаик) в
трехмерном гиперпространстве ![]() , обладающих определенным
типом симметрии. Предваряя эти результаты, начнем с гиперкомплексных чисел.
, обладающих определенным
типом симметрии. Предваряя эти результаты, начнем с гиперкомплексных чисел.
9.1. Гиперкомплексные числа и кватернионы
Гиперкомплексные числа имеют вид (см., например, [24])
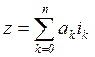 , (9.1)
, (9.1)
где ![]() – произвольные
действительные числа (
– произвольные
действительные числа (![]() ), a
), a ![]() – некоторые символы, которые называют «мнимыми единицами». Иногда говорят,
что имеется
– некоторые символы, которые называют «мнимыми единицами». Иногда говорят,
что имеется ![]() -мерное пространство с базисом
-мерное пространство с базисом ![]() над полем вещественных чисел
над полем вещественных чисел ![]() . Над выражениями (9.1) будем производить
действия сложения (вычитания) по формулам
. Над выражениями (9.1) будем производить
действия сложения (вычитания) по формулам
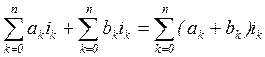 .
.
Для определения «умножения»
необходимо задать «таблицу умножения», т. е. указать, чему равны всевозможные
произведения ![]() ,
, ![]() . Задание разных «таблиц умножения» приводит к
разным системам гиперкомплексных
чисел. Например, в случае комплексных чисел, когда
. Задание разных «таблиц умножения» приводит к
разным системам гиперкомплексных
чисел. Например, в случае комплексных чисел, когда ![]() , таблица
умножения сводится к единственному равенству
, таблица
умножения сводится к единственному равенству ![]() . В
случае
. В
случае ![]() определим таблицу умножения следующим
образом:
определим таблицу умножения следующим
образом:
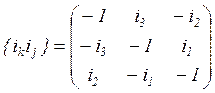 . (9.2)
. (9.2)
Таким образом, ![]() и
умножение не коммутативно. Введем обозначение
и
умножение не коммутативно. Введем обозначение ![]() ,
, ![]() ,
, ![]() . Тогда
из (9.2) следует
. Тогда
из (9.2) следует ![]() . В этом случае гиперкомплексные
числа
. В этом случае гиперкомплексные
числа
![]() ,
, ![]() (9.3)
(9.3)
называются кватернионами. Соотношение (9.3) можно представить в виде
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Здесь через ![]() обозначено пространство комплексных чисел.
Через
обозначено пространство комплексных чисел.
Через ![]() будем обозначать пространство кватернионов.
Для любого
будем обозначать пространство кватернионов.
Для любого ![]() (также как и в пространстве
(также как и в пространстве ![]() ) можно определить сопряженный кватернион:
) можно определить сопряженный кватернион: ![]() . По аналогии с
комплексными числами число
. По аналогии с
комплексными числами число ![]() называется модулем кватерниона
называется модулем кватерниона
![]() . Справедливы следующие соотношения
. Справедливы следующие соотношения ![]() . Наконец, гиперкомплексная система кватернионов – это система с делением.
. Наконец, гиперкомплексная система кватернионов – это система с делением.
Гиперкомплексные системы и, в частности, кватернионы хорошо известны алгебраистам. Здесь мы будем использовать гиперкомплексную систему при рассмотрении «динамической задачи» об отображениях, обобщающих известное отображение Жюлиа.
9.2. Отображение Жюлиа в гиперпространстве
Рассмотрим отображение (дискретную динамическую систему)
![]() ,
, ![]() ,
, ![]() , (9.4)
, (9.4)
где ![]() – полином степени
– полином степени ![]() ,
коэффициенты которого, вообще говоря, являются кватернионами. В качестве
примера такого отображения рассмотрим квадратичное
отображение
,
коэффициенты которого, вообще говоря, являются кватернионами. В качестве
примера такого отображения рассмотрим квадратичное
отображение
![]() ,
, ![]() , (9.5)
, (9.5)
где ![]() – вещественные параметры. Многое из того,
о чем мы будем говорить, переносится на отображения
– вещественные параметры. Многое из того,
о чем мы будем говорить, переносится на отображения
![]() , где
, где ![]() .
.
Исследование (9.5) сведем к анализу траекторий отображения
![]() ,
, ![]() , (9.6)
, (9.6)
где ![]() – подпространство пространства
– подпространство пространства ![]() , элементами которого являются всевозможные гиперкомплексные числа
, элементами которого являются всевозможные гиперкомплексные числа ![]() ,
, ![]() . Разделяя в (9.5)
действительную и мнимые части (
. Разделяя в (9.5)
действительную и мнимые части (![]() ) приходим к
вещественному отображению в
) приходим к
вещественному отображению в ![]() :
:
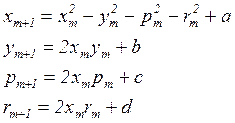 (9.7)
(9.7)
Если ![]() и
и ![]() , то
, то ![]() ,
, ![]() . В этом
случае отображение (9.7) сводится к
. В этом
случае отображение (9.7) сводится к ![]() -х мерному отображению
(9.6):
-х мерному отображению
(9.6):
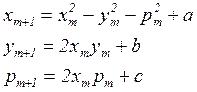 (9.8)
(9.8)
А именно, это
отображение мы и рассмотрим в данном разделе. Будем называть его ![]() -х
мерным отображением Жюлиа и обозначать через
-х
мерным отображением Жюлиа и обозначать через ![]() . Если в
(9.8) положить
. Если в
(9.8) положить ![]() и
и ![]() , то это отображение в свою очередь
сведется к рассмотренному в гл. 6–7 двухмерному отображению Жюлиа
, то это отображение в свою очередь
сведется к рассмотренному в гл. 6–7 двухмерному отображению Жюлиа ![]() :
:
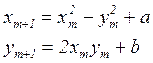 (9.9)
(9.9)
Наконец, если ![]() и
и ![]() , то
(9.9) приводит к одномерному (логистическому – logistic map)
отображению
, то
(9.9) приводит к одномерному (логистическому – logistic map)
отображению ![]() :
:
![]() (9.10)
(9.10)
9.2.1. Свойства отображения ![]()
Как мы заметили, справедливо
Свойство 1.Если ![]() и
и ![]() , то
, то ![]() сводится
к
сводится
к ![]() .
.
Далее приведем другие свойства отображения
![]() ,
снабжая их, по возможности, доказательством.
,
снабжая их, по возможности, доказательством.
Свойство 2.Обратное отображение ![]() имеет
вид
имеет
вид
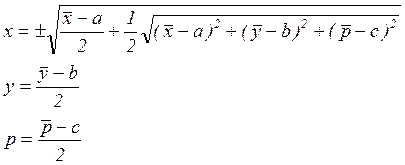 (9.11)
(9.11)
Свойство 3.При ![]() отображение (9.8) имеет
в ограниченной части пространства
отображение (9.8) имеет
в ограниченной части пространства ![]() две неподвижных точки
две неподвижных точки ![]() и
и ![]() , где
, где 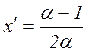 ,
, ![]() ,
, ![]() и
и 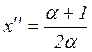 ,
, ![]() ,
, ![]() ,
, 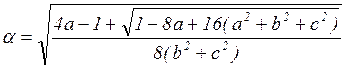 .
.
Свойство 4. При выполнении условий ![]() ,
, ![]() ,
, ![]() неподвижная точка
неподвижная точка ![]() устойчивая, а
устойчивая, а ![]() всегда неустойчивая.
всегда неустойчивая.
Доказательство этого
свойства следует из того, что для точки ![]() при указанных условиях мультипликаторы
при указанных условиях мультипликаторы ![]() лежат внутри единичного круга на комплексной
плоскости (
лежат внутри единичного круга на комплексной
плоскости (![]() ,
,![]() ), а для
), а для ![]() имеется корень вне единичной окружности.
Здесь
имеется корень вне единичной окружности.
Здесь ![]() – корни характеристического уравнения
– корни характеристического уравнения
![]() , где
, где ![]() – одна из неподвижных точек.
– одна из неподвижных точек.
Свойство 5. При ![]() и
и ![]() существует единственная устойчивая
неподвижная точка
существует единственная устойчивая
неподвижная точка 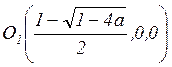 и единственная неустойчивая
неподвижная точка
и единственная неустойчивая
неподвижная точка 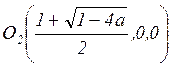 . При
. При ![]() эти неподвижные точки сливаются и при
эти неподвижные точки сливаются и при ![]() исчезают; от сложной точки
исчезают; от сложной точки ![]() родится инвариантное множество – цикл:
родится инвариантное множество – цикл: 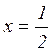 ,
, 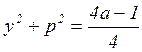 . На интервале
. На интервале
![]() имеется счетное множество подынтервалов существования устойчивых периодических точек.
имеется счетное множество подынтервалов существования устойчивых периодических точек.
Доказательство
существования счетного множества подынтервалов с устойчивыми периодическими точками следует из редукции ![]() к логистическому отображению
к логистическому отображению ![]() (9.10).
(9.10).
Обозначим через ![]() замыкание
множества отталкивающих (неустойчивых) точек отображения
замыкание
множества отталкивающих (неустойчивых) точек отображения ![]() ,
, ![]() , т.е.
если
, т.е.
если ![]() , то
, то 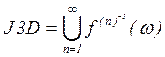 .
.
Иногда это множество мы будем обозначать
через ![]() . Множество
. Множество ![]() является
является
![]() -х мерным аналогом множества Жюлиа
-х мерным аналогом множества Жюлиа ![]() , Как мы заметили
выше, это множество может не содержать неустойчивую неподвижную точку
(из-за ее отсутствия).
, Как мы заметили
выше, это множество может не содержать неустойчивую неподвижную точку
(из-за ее отсутствия).
Свойство 6. При ![]() (
(![]() ) множество
) множество ![]() принадлежит
сфере
принадлежит
сфере ![]() и идуцированное на ней отображение является
хаотическим.
и идуцированное на ней отображение является
хаотическим.
Действительно, ![]() и сфера
является отталкивающим множеством. Так как в силу (8) имеем
и сфера
является отталкивающим множеством. Так как в силу (8) имеем 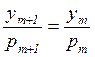 , то множество
, то множество ![]() расслаивается на окружности единичного радиуса с
центром в начале координат, лежащие в плоскости, проходящей через ось
расслаивается на окружности единичного радиуса с
центром в начале координат, лежащие в плоскости, проходящей через ось ![]() и прямую
и прямую 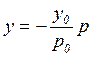 . Отображение
на окружности
. Отображение
на окружности ![]() ,
, ![]() , как известно
[18], хаотично. Этот факт указывает на возможность хаотичности отображения
, как известно
[18], хаотично. Этот факт указывает на возможность хаотичности отображения ![]() на множестве
на множестве ![]() при
при ![]() .
.
Свойство 7. Множество ![]() симметрично
относительно осей
симметрично
относительно осей ![]() ,
,
![]() и при малых
и при малых ![]() лежит на
поверхности вращения относительно
лежит на
поверхности вращения относительно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.