Введение во фрактальную динамику

возможно  будет всей комплексной плоскостью; например, если .)

Утверждение 6.2.  не пусто.

Доказательство. Предположим, что . Тогда, для любого  семейство  нормально на открытом круге  с центром в начале координат и радиусом  (так как замкнутый диск  является компактным, он может быть покрыт конечным числом открытых множеств, на которых  нормальна). Так как  – полином, взяв  достаточно большим, получим, что  содержит точку , для которой  и также содержит неподвижную точку  преобразования  для всех . Таким образом, невозможно для любой подпоследовательности  равномерно сходиться либо к ограниченной функции, либо к бесконечности на любом компактном подмножестве , которое содержит как , так и , опровергая нормальность .

Утверждение 6.3. является инвариантным как для , так и для , то есть .

Доказательство. Мы покажем, что дополнение  – инвариант. Пусть  – открытое множество с  нормальной на . Так как  непрерывна, то  – открытое множество. Пусть  является подпоследовательностью . Тогда  имеет подпоследовательность , которая равномерно сходится на компактных подмножествах . Таким образом, если  – компактное подмножество , то  равномерно сходится на компактном множестве , поэтому  равномерно сходится на . Таким образом,  нормальна на , поэтому . Другие требуемые включения могут быть получены аналогичным способом, используя то, что полином  – открытое отображение, то есть, что  открыто, когда  открыто.

Утверждение 6.4.  для любого положительного целого .

Доказательство. Снова мы работаем с дополнением . Очевидно, если любая последовательность  имеет подпоследовательность, равномерно сходящуюся на данном множестве, то же самое верно для . Таким образом, .

Если  компактно и  семейство функций, равномерно сходящихся на  либо к ограниченной функции, либо к , то тоже самое верно для  для любого полинома . Таким образом, если  нормально на любом открытом множестве , то это справедливо и для , . Но любая подпоследовательность  содержит бесконечную подпоследовательность  для некоторого целого  с , которая имеет подпоследовательность, равномерно сходящуюся на компактных подмножествах . Отсюда  нормальна, поэтому .

Наш следующий результат утверждает, что  есть «перемешивающее» преобразование, то есть окрестности точек в  покрывают почти всю комплексную плоскость при итерациях .

Утверждение 6.5.Пусть  – полином,  и пусть  – любая окрестность . Тогда 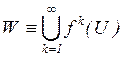 совпадает с , исключая, возможно, единственную точку. Любая такая исключительная точка не принадлежит  и не зависит от  и .

Доказательство. По определению  семейство  не нормально в точке , поэтому первая часть непосредственно вытекает из теоремы Монтеля.

Предположим, что . Если , то, так как , то . Так как  состоит из самое большее одной точки, то . Отсюда,  – полином степени  такой, что единственное решение  – это , и  для некоторой константы .

Если  достаточно близка к , то  при  и сходимость имеет место, например, на . Таким образом,  нормальна в точке , поэтому исключительная точка . Очевидно,  зависит только от полинома . (Фактически, если  не содержит точку  из , то  – это окружность с центром в точке  и радиуса ).

Следующее утверждение (следствие) является основой многих компьютерных картинок множеств Жюлиа.

Утверждение 6.6.

(а)     Следующее свойство выполняется для всех  с, самое большее, одним исключением: если  – открытое множество, пересекающее , то  пересекает  для бесконечно многих значений .

(б)          Если , то  – это замыкание .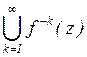

Доказательство.

(а)     При условии, что  не является исключительной точкой утверждения 6.5, . Поэтому  пересекает  для некоторого . Используя это повторно, мы получим бесконечную последовательность  с  пересекающей .

(б)     Если , то  no утверждению 6.3, так что 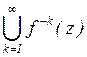 и, поэтому, его замыкание содержится в замкнутом множестве . С другой стороны, если  – открытое множество, содержащее , то  пересекает  для некоторого  по пункту (a);  не может быть исключительной точкой по утверждению 6.5.

Другое непосредственное следствие из утверждения 6.5 – это то, что  не может быть «слишком толстым».

Утверждение 6.7. Если  – полипом, то  имеет пустую внутренность.

Доказательство. Предположим,  содержит открытое множество . Тогда  для всех , по утверждению 6.3, поэтому 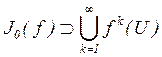. По утверждению 6.5,  это вся плоскость , исключая, возможно, одну точку. Это опровергает утверждение 6.1 об ограниченности .

Утверждение 6.8.  – совершенное множество (то есть замкнутое и не имеет изолированных точек) и поэтому несчетно.

Доказательство.

Пусть  и пусть  будет окрестностью . Мы должны показать, что  содержит другие точки . Мы рассмотрим эти три случая отдельно.

(1)      не является неподвижной или периодической точкой . По утверждению 6.3 и утверждению 6.6(б),  содержит точку  для некоторого , и эта точка должна быть отлична от .

(2)     . Если  не имеет решения отличного от , тогда так же, как и в доказательстве утверждения 6.5, . Таким образом, существует  с . По утверждению 6.6(б)  содержит точку  для некоторого . Любая такая точка находится в  с помощью обратного инварианта и отличается от , так как .

(3)      для некоторого . По утверждению 6.4, , поэтому, применяя (6.2) к , мы видим, что  содержит точки  другие, чем .

Мы можем теперь доказать главный результат этого раздела, что  – множество точек ненормальности  (это точно то же самое, что и , замыкание отталкивающих периодических точек ).

Утверждение 6.9. Если  – полином, тогда .

Доказательство. Пусть  будет отталкивающей периодической точкой  периода , поэтому  – отталкивающая неподвижная точка . Предположим, что  нормально в точке , тогда  имеет открытую окрестность , на которой подпоследовательность  сходится к конечной аналитической функции  (она не может сходиться к , так как  для всех ). По известному результату из комплексного анализа производные также сходятся, , если . Однако , так как  – это отталкивающая неподвижная точка и . Это опровергает конечность , поэтому  не может быть нормальным в . Таким образом, , no утверждению 6.4. Так как  замкнуто, то отсюда следует .

Пусть . Предположим, что . Тогда существует открытая окрестность  точки , в которой мы можем найти локальную аналитическую обратную функцию