Министерство образования и науки РФ
ГОУВПО «Комсомольский-на-Амуре государственный технический университет»
Кафедра МОП ЭВМ
Лабораторная работа №4
По дисциплине «Компьютерная графика»
Выполнил: Николусь П.А.
Группа: 4ВС-1
Проверила: Михайлова Н.Н.
Комсомольск-на-Амуре
2006
Задание. Вывести на экран изображение
поверхности ![]() с удалением невидимых
линий. Удаление невидимых линий осуществляется с использованием алгоритма
плавающего горизонта. Рассматривается параллельная проекция.
с удалением невидимых
линий. Удаление невидимых линий осуществляется с использованием алгоритма
плавающего горизонта. Рассматривается параллельная проекция.
Рассмотрим параллельную проекцию трехмерного пространства на плоскость Oyz в направлении вектора u=(-1,-1,-1). Плоскость Oyz можно задать векторами u1=(0,1,0), u2=(0,0,1).
Смешанное произведение (u1,u2,u) равно -1. Поэтому
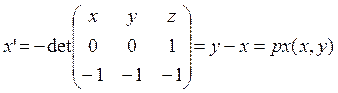 ,
, 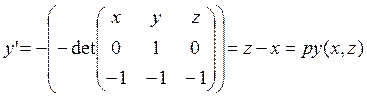 .
.
Получаем экранные координаты:
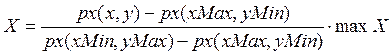 ,
,
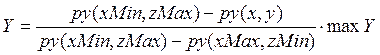 .
.
Листинг программы:
float px(float x, float y) {return y - x;}
float py(float x, float z) {return z - x;}
float z(float x, float y) {return x * y / (x * x + y * y + 1);}
void horizon(int, int, int, int, int *, int *);
TCanvas *DC;
void __fastcall TForm1::FormResize(TObject *Sender)
{
DC = Form1->Canvas;
DC->Pen->Width = 2;
int nx = 10, ny = 10, maxX = Form1->ClientWidth,
maxY = Form1->ClientHeight, *tophor = new int[maxX+2],
*bothor = new int[maxX+2], x0, y0, x1, y1, x2, y2, i, j;
float xMin = -1, xMax = 1, yMin = -1, yMax = 1, zMin = -1, zMax = 1,
minxOx, maxxOx, minyOy, maxyOy, hx, hy, x, y;
TRect rect;
rect.left = 0;
rect.right = maxX;
rect.top = 0;
rect.bottom = maxY;
DC->FillRect(rect);
for (i = 0; i <= maxX; ++i)
bothor[i] = maxY, tophor[i] = 0;
minxOx = px(xMax, yMin);
maxxOx = px(xMin, yMax);
minyOy = py(xMax, zMin);
maxyOy = py(xMin, zMax);
hx = (xMax - xMin) / nx;
hy = (yMax - yMin) / ny;
for (x = xMax, i = 0; i < nx; x -= hx, ++i)
{
x0 = maxX * (px(x, yMax) - minxOx) / (maxxOx - minxOx);
y0 = maxY * (maxyOy - py(x, z(x, yMax))) / (maxyOy - minyOy);
for (y = yMax - hy, j = 0; j < ny; y -= hy, ++j)
{
x1 = maxX * (px(x, y) - minxOx) / (maxxOx - minxOx);
y1 = maxY * (maxyOy - py(x, z(x, y))) / (maxyOy - minyOy);
x2 = maxX * (px(x - hx, y + hy) - minxOx) / (maxxOx - minxOx);
y2 = maxY * (maxyOy - py(x - hx, z(x - hx, y + hy))) / (maxyOy - minyOy);
horizon(x0, y0, x1, y1, bothor, tophor);
horizon(x0, y0, x2, y2, bothor, tophor);
x0 = x1;
y0 = y1;
}
x2 = maxX * (px(x - hx, y + hy) - minxOx) / (maxxOx - minxOx);
y2 = maxY * (maxyOy - py(x - hx, z(x - hx, y + hy))) / (maxyOy - minyOy);
horizon(x0, y0, x2, y2, bothor, tophor);
}
x0 = maxX * (px(xMin, yMax) - minxOx) / (maxxOx - minxOx);
y0 = maxY * (maxyOy - py(xMin, z(xMin, yMax))) / (maxyOy - minyOy);
for (y = yMax - hy, j = 0; j < ny; y -= hy, ++j)
{
x1 = maxX * (px(xMin, y) - minxOx) / (maxxOx - minxOx);
y1 = maxY * (maxyOy - py(xMin, z(xMin, y))) / (maxyOy - minyOy);
horizon(x0, y0, x1, y1, bothor, tophor);
x0 = x1;
y0 = y1;
}
DC->MoveTo(maxX * (px(xMax, yMin) - minxOx) / (maxxOx - minxOx) + 1, maxY * (maxyOy - py(xMax, zMax)) / (maxyOy - minyOy));
DC->LineTo(maxX * (px(xMin, yMin) - minxOx) / (maxxOx - minxOx), maxY * (maxyOy - py(xMin, zMax)) / (maxyOy - minyOy) + 1);
DC->LineTo(maxX * (px(xMin, yMax) - minxOx) / (maxxOx - minxOx)-1, maxY * (maxyOy - py(xMin, zMax)) / (maxyOy - minyOy) + 1);
DC->LineTo(maxX * (px(xMin, yMax) - minxOx) / (maxxOx - minxOx)-1, maxY * (maxyOy - py(xMin, zMin)) / (maxyOy - minyOy));
DC->LineTo(maxX * (px(xMax, yMax) - minxOx) / (maxxOx - minxOx), maxY * (maxyOy - py(xMax, zMin)) / (maxyOy - minyOy) - 1);
DC->LineTo(maxX * (px(xMax, yMin) - minxOx) / (maxxOx - minxOx), maxY * (maxyOy - py(xMax, zMin)) / (maxyOy - minyOy) - 1);
DC->LineTo(maxX * (px(xMax, yMin) - minxOx) / (maxxOx - minxOx) + 1, maxY * (maxyOy - py(xMax, zMax)) / (maxyOy - minyOy));
DC->LineTo(maxX * (px(xMax, yMax) - minxOx) / (maxxOx - minxOx) + 1, maxY * (maxyOy - py(xMax, zMax)) / (maxyOy - minyOy));
DC->LineTo(maxX * (px(xMax, yMax) - minxOx) / (maxxOx - minxOx) + 1, maxY * (maxyOy - py(xMax, zMin)) / (maxyOy - minyOy));
DC->LineTo(maxX * (px(xMax, yMax) - minxOx) / (maxxOx - minxOx) + 1, maxY * (maxyOy - py(xMax, zMax)) / (maxyOy - minyOy));
DC->LineTo(maxX * (px(xMin, yMax) - minxOx) / (maxxOx - minxOx) + 1, maxY * (maxyOy - py(xMin, zMax)) / (maxyOy - minyOy));
horizon(maxX * (px(xMin, yMin) - minxOx) / (maxxOx - minxOx)-1, maxY * (maxyOy - py(xMin, zMin)) / (maxyOy - minyOy), maxX * (px(xMax, yMin) - minxOx) / (maxxOx - minxOx), maxY * (maxyOy - py(xMax, zMin)) / (maxyOy - minyOy), bothor, tophor);
horizon(maxX * (px(xMin, yMin) - minxOx) / (maxxOx - minxOx)-1, maxY * (maxyOy - py(xMin, zMin)) / (maxyOy - minyOy), maxX * (px(xMin, yMin) - minxOx) / (maxxOx - minxOx), maxY * (maxyOy - py(xMin, zMax)) / (maxyOy - minyOy), bothor, tophor);
horizon(maxX * (px(xMin, yMin) - minxOx) / (maxxOx - minxOx)-1, maxY * (maxyOy - py(xMin, zMin)) / (maxyOy - minyOy), maxX * (px(xMin, yMax) - minxOx) / (maxxOx - minxOx), maxY * (maxyOy - py(xMin, zMin)) / (maxyOy - minyOy), bothor, tophor);
delete tophor;
delete bothor;
}
void horizon(int x0, int y0, int x1, int y1, int *bothor, int *tophor)
{
int n = abs(x1 - x0);
if (n < abs(y1 - y0))
n = abs(y1 - y0);
float nx = (0. + x1 - x0) / n;
float ny = (0. + y1 - y0) / n;
float curx = x0 + 0.5;
float cury = y0 + 0.5;
for (int i = 0 ; i <= n; ++i, curx += nx, cury +=ny)
{
if (cury < bothor[(int) curx] || cury > tophor[(int) curx])
{
(cury < bothor[(int) curx]) ? (bothor[(int) curx] = cury) : 0;
(cury > tophor[(int) curx]) ? (tophor[(int) curx] = cury) : 0;
DC->MoveTo(curx, cury);
DC->LineTo(curx, cury);
}
}
}
Выполнение программы:
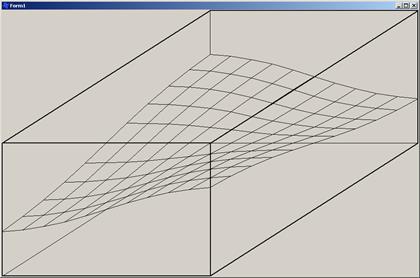
Список литературы:
1. Хусаинов А.А., Михайлова Н.Н. Алгоритмы машинной графики и их реализация на языке Си: Учеб. пособие. – Комсомольск-на-Амуре: Комсомольский-на-Амуре гос. техн. ун-т, 1999. – 65 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.