Вывести график функции. Построить алгоритм и разработать программу для решения задачи

которые соответствуют четырем страницам видеопамяти, например, EGA, EGALO или VGA, VGALO. Затем в цикле поочередно делаем страницы видеопамяти активными и на каждую выводим изображение таким образом, чтобы одно получалось из другого поворотом на угол p/8. А потом в цикле поочередно делаем страницы видимыми, что и создает иллюзию вращения. Рекомендуется ставить задержку с помощью функции delay перед выводом каждой видимой страницы.

В задачах 8 и 10 изображение рекомендуется разбить на четыре одинаковых сектора. Для изображения каждого сектора использовать четыре цвета. Например, в задаче 8 будет 16 закрашенных секторов, но использоваться будет всего четыре цвета. Например, расположение цветов в круге: красный, голубой, зеленый, желтый, красный, голубой, зеленый, желтый, красный, голубой, зеленый, желтый, красный, голубой, зеленый, желтый.

Задача 11. Эта задача решается с помощью функций getimage и putimage. Предположим, что мы располагаем памятью, достаточной для того, чтобы запомнить весь экран. Тогда задача решается следующим образом. Сначала с помощью функции getimage запоминаем изображение на экране. Затем с помощью функции putimage при способе наложения изображения на экран OR_PUT размещаем на экране это же изображение, но со сдвигом на один пиксел вправо и вниз. Таким образом на экране останется старое изображение и будет выведена его копия, но со сдвигом на один пиксел вправо и вниз. За счет этого получится новое изображение, в котором толщина каждой линии увеличится в два раза. Если же памяти недостаточно для того, чтобы запомнить все изображение, то разбиваем экран на равные прямоугольники (например, на 16 прямоугольников) и осуществляем описанные выше операции поочередно для каждого прямоугольника.

Задача 12. Прежде всего сформулируем критерий пересечения двух отрезков в одной точке. Два отрезка (рис. 20) пересекаются в одной точке, если одновременно выполняются два условия:

1)  концы первого отрезка находятся по разные стороны от прямой, проходящей через второй отрезок;

2)  концы второго отрезка находятся по разные стороны от прямой, проходящей через первый отрезок.

На рис. 20 один отрезок соединяет точки (x₀, y₀) и (x₁, y₁). Прямую, проходящую через эти точки, обозначим f1. Второй отрезок проходит через точки (x₂, y₂) и (x₃, y₃). Прямую, проходящую через эти точки, обозначим f2. Запишем уравнение прямой, проходящей через точки (x₀, y₀) и (x₁, y₁), в виде f(x,y)= 0, а именно: f(x,y)= Dy(x-x₀) - Dx(y-y₀) = 0, где Dx = x₁-x₀ и Dy=y₁-y₀. Все точки области, содержащей отрезок прямой f(x,y)= 0, можно разбить на три множества: множество точек, принадлежащих прямой (для этих точек выполняется условие f(x,y)= 0), множество точек, расположенных справа от прямой (для них выполнено условие f(x,y) > 0), и множество точек, расположенных слева от прямой (для них выполнено условие f(x,y) < 0). Таким образом, для точек, расположенных по разные стороны от прямой, функция f(x,y) имеет разные знаки.

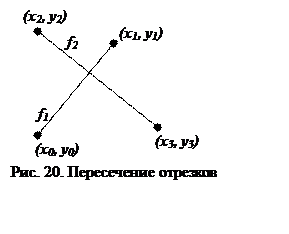В обозначениях рис. 20 критерий пересечения отрезков можно определить следующим образом: в точках (x₀, y₀) и (x₁, y₁) функция f₂ принимает значения разных знаков (f₂(x₀,y₀)·f₂(x₁,y₁)<0) и одновременно в точках (x₂, y₂) и (x₃, y₃) функция f₁ принимает значения разных знаков (f₁(x₂,y₂)·f₁(x₃,y)<0).

Задача 13. Решение задачи 13 опирается на критерий пересечения отрезков, сформулированный в задаче 12. Сформулируем критерий выпуклости. Многоугольник (x₀, y₀), …, (x_n-1, y_n-1) является выпуклым, если для каждой его стороны (x_i, y_i), (x_i+1, y_i+1), 0≤ i ≤ n-2 выполнено следующее условие: все остальные (n-2) вершины