Информатика и выч. техника \ Компьютерный дизайн

Краткие сведения из теории множеств

Страницы работы

5 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Приложение

Глава 10. Краткие сведения из теории множеств

Следуя, например, [5], рассмотрим некоторое множество (совокупность) элементов какой-либо природы. Обозначим его через , а его элементы через .

Запись означает, что является элементом множества , означает, что не является элементом множества .

Определение 10.1: Пусть – два множества. Если каждый элемент входит также в , то говорят, что – подмножество и обозначают: .

Например, (множество натуральных чисел), ().

Определение 10.2: Равными называют одинаковые множества: (все элементы совпадают с элементами ).

Пример множества: множество вещественных корней алгебраического уравнения. Однако такие уравнения могут не иметь вещественных корней, поэтому вводят понятие пустого множества: . Пустое множество является подмножеством любого множества.

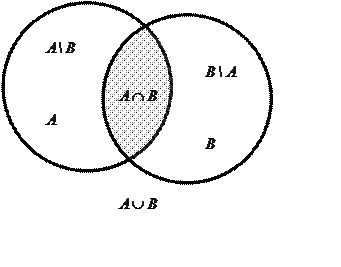
Рис. 10.1

Определение 10.3: Суммой двух множеств и называется множество , которое состоит из всех элементов, входящих, по крайней мере, в одно из множеств или .

Определение обобщается для произвольного числа множеств: .

Определение 10.4: Разностью (дополнением к множеству ) называется подмножество множества , не входящее в .

Определение 10.5: Пересечением двух множеств и называется множество (обозначаемое ), состоящее из всех элементов, которые входят и в , и в .

Очевидно: .

Если , то .

Дистрибутивность: .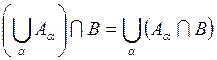

10.0.1. Мощность множества

Конечные множества можно легко сравнить между собой, например, с помощью подсчета. Пример: сравнить число студентов, пришедших в аудиторию, с числом стульев.

Определение 10.6: Пусть даны два множества и . Говорят, что между их элементами установлено взаимно однозначное соответствие, если указало правило, по которому каждому элементу соответствует один элемент , называемый образом элемента «», причем выполнены следующие два условия:

a) любые два элемента из имеют различные образы;

b) любой элемент из является образом некоторого элемента из .

Определение 10.7: Два множества и называются эквивалентными или имеющими одинаковую мощность (обозначается ), если между их элементами может быть установлено взаимно однозначное соответствие.

Очевидно, два конечных множества эквивалентны тогда и только тогда, когда они состоят из одного числа элементов.

10.0.2. Примеры эквивалентных множеств

1. Множество всех натуральных чисел и множество всех целых отрицательных чисел ().

2. 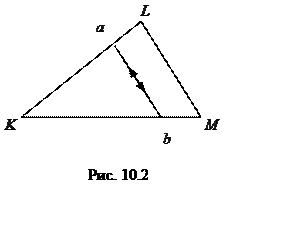Множество и множество всех положительных четных целых чисел: , , .

3. Множество всех вещественных чисел и множество всех вещественных чисел из интервала (, , ).

4. Пусть – треугольник произвольной формы, а и – множества всех точек на сторонах и соответственно.

Рис. 10.3

Справедливы свойства:

1. Если , , то .

2. Если множество , причем слагаемые попарно не имеют общих элементов, а множество и слагаемые также попарно не имеют общих элементов, и если при каждом , то .

10.1. Счетные множества

Определение 10.8:Множество называется счетным, если оно эквивалентно множеству всех натуральных чисел.

То есть, если , то – счетно. Согласно [5], справедливы следующие теоремы:

Теорема 10.1:Сумма счетного множества счетных множеств – тоже счетное множество.

Теорема 10.2:Множество всех рациональных чисел счетно.

Теорема 10.3:Множество всех алгебраических полиномов с рациональными коэффициентами счетно.

10.2. Множества мощности континуума

Теорема 10.4:Множество всех вещественных чисел, содержащихся в отрезке , несчетно.

Определение 10.9:Говорят, что множество имеет мощность континуума (обозначение: «»), если оно эквивалентно множеству всех чисел из отрезка .

Замечание 10.1:Любой промежуток имеет мощность «» ().

Следствие 10.1:Множество всех вещественных чисел имеет мощность «».

Теорема 10.5:Множество всех иррациональных чисел имеет мощность «».

Можно рассмотреть вопрос о сравнении мощностей (подробности см., например, в [5]).

Континуум гипотеза 10.1:Не существует множества промежуточной мощности между мощностью счетного множества и мощностью «», но существует множество мощности большей «».

10.3. Кольца и алгебры множеств

Определение 10.10:Пусть – произвольное множество. Непустая совокупность некоторых его подмножеств называется кольцом, если для любых :

, .

Определение 10.11:Непустая совокупность подмножеств множества называется алгеброй, если она удовлетворяет следующим условиям:

если , то ;

если , то и его дополнение .

Теорема 10.6:Для того чтобы совокупность подмножеств множества была алгеброй, необходимо и достаточно, чтобы она была кольцом и чтобы .

Определение 10.12:Непустая совокупность подмножеств множества называется -кольцом, если она – кольцо, замкнутое по отношению к операции сложения не только конечного, но и счетного семейства множеств, т. е.:

1. из условия () следует, что ;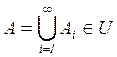

2. из условия следует, что .

Определение 10.13:Непустая совокупность подмножеств множества называется -алгеброй, если она удовлетворяет условию 1 из определения -кольца и условию 2 из определения алгебры .

Утверждение 10.1:Для того, чтобы совокупность была -алгеброй, необходимо и достаточно, чтобы она была -кольцом и чтобы .