Плоская машинная графика

2. ПЛОСКАЯ МАШИННАЯ ГРАФИКА

В этой главе будут описаны алгоритмы генерации точек прямолинейных и криволинейных отрезков и алгоритмы  заполнения  областей экрана.

Литература: /1-4, 7-8, 10, 12, 17-20/.

2.1. АЛГОРИТМЫ ГЕНЕРАЦИИ ТОЧЕК ПРЯМОЛИНЕЙНОГО ОТРЕЗКА

Опишем сначала алгоритмы, известные как цифровые дифференциальные анализаторы (сокращенно ЦДА). Координаты точек отрезка с концами (x₀ ,y₀) и (x₁ ,y₁), лежащего в плоскости R², принимают значения

x = x₀ + t(x₁ - x₀),

y = y₀ + t(y₁ - y₀),

где 0 £ t £ 1 . Поэтому, выбрав достаточно малое число e > 0 и придавая координатам x и y приращения e×(x₁ - x₀) и e×(y₁ - y₀), мы могли бы строить точки отрезка, если бы дисплей обладал абсолютной точностью. Поскольку абсолютной точности нет, мы вынуждены использовать округления значений x и y , полученных после очередной пары приращений, с точностью до целых чисел.

Положим Dx = x₁ - x₀, Dy = y₁ - y₀. Так как округление произвольного вещественного числа r Î R равно целой части числа 0.5 + r, с помощью данного алгоритма (при условии, что 1/e является целым положительным числом) генерируются точки, имеющие координаты

X = (int)(0.5 + x₀ + e×i×Dx),

Y = (int)(0.5 + y₀ + e×i×Dy),

где  i  пробегает значения i = 0, 1,...,1/e.

Для того чтобы каждый раз не делать округлений, заводятся два аккумулятора - один для дробной части числа x, другой – для дробной части числа y. Значения приращений, оба по модулю меньшие единицы, на каждом шаге прибавляются к дробным частям. Если один из аккумуляторов переполнился, в том смысле, что его значение стало больше или равно 1 (либо меньше 0), то от этого аккумулятора вычитается (либо прибавляется к аккумулятору, в зависимости от направления движения) единица, а значение соответствующей целочисленной координаты увеличивается (либо уменьшается) на  единицу и ставится точка (X,Y). Вместо дробных частей в аккумуляторах следует хранить дробные части, умноженные на такое натуральное M, что K = e×M - целое число. В этом случае аккумуляторы получают приращения K×(x₁-x₀) и K×(y₁-y₀) , вместо e×(x₁-x₀) и e×(y₁-y₀). Поскольку

|e×(x₁-x₀)| £ 1, |e×(y₁-y₀) |£ 1,

содержимое каждого аккумулятора будет целым числом, лежащим в диапазоне от 0 до M-1. Последовательность генерируемых точек зависит от выбора числа e. Мы рассмотрим здесь два случая.

1) Симметричный ЦДА. Пусть n > 0 - такое натуральное число, что при любых значениях (x₀, y₀), (x₁, y₁) координат пикселов выполнено неравенство

2^n-1 £ max {|x₁-x₀|, |y₁-y₀|} < 2 ⁿ. Полагая e = 1/2ⁿ, получаем ЦДА, называемый симметричным. Для адаптеров CGA, EGA и VGA число n равно 10. Полагая M = 1024, находим K = 1. Начальные значения аккумуляторов равны 512. Аккумуляторы получают приращения x₁-x₀ и y₁-y₀. Если значение какого-нибудь аккумулятора стало меньше 0, либо больше или равно 1024, то соответствующая координата изменяется, к аккумулятору прибавляется приращение и ставится точка. Приходим к такой реализации алгоритма:

Программа

//Генерация точек отрезка методом симметричного ЦДА

#include <stdio.h>

#include <conio.h>

#include <graphics.h>

int x0, y0; //Координаты центра системы координат относит. лев. верх. угла

int hx=3, hy=3; //1/2 ширины и длины пиксела

//Функция определения знака целого числа

int sign (int r)

{

if (r>0) return 1;

else if (r<0) return -1;

else return 0;

}

//Вывод "крупного" пиксела на экран

void point( int ix, int iy )

{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1,x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}

//Генерация и вывод точек отрезка

void symcda(int x0, int y0, int x1, int y1)

{

int res_x=512, res_y=512;  //Инициализация аккумуляторов

int x=x0, y=y0; //Начало отрезка

int dx=x1-x0, dy=y1-y0;

int ex=sign(dx), ey=sign(dy);

point (x,y);               //Выводим первый пиксел

while (!(x==x1 && y==y1))  //Цикл пока не дойдем до конца отрезка

{

res_x+=dx;

//Проверка аккумулятора

if (res_x>=1024 || res_x <0)

{

x+=ex;

point(x,y);//Вывод очередного пиксела

res_x-=ex*1024;

}

res_y+=dy;

//Проверка аккумулятора

if (res_y>=1024 || res_y<0)

{

y+=ey;

point(x,y);//Вывод очередного пиксела

res_y-=ey*1024;

}

}

}

void main()

{

int gdriver=DETECT, gmode;

initgraph (&gdriver, &gmode, "");

x0=getmaxx()/2; y0=getmaxy()/2;

moveto(0,y0); linerel(getmaxx(),0);

moveto(x0,0); linerel(0, getmaxy());

symcda(0,0,5,3);  //Вывод отрезка

getch();          //Ожидание нажатия клавиши

closegraph();     //Выключение графического режима

}

Будут выведены точки (рис. 1) (0,0), (1,0), (1,1), (2,1), …

 

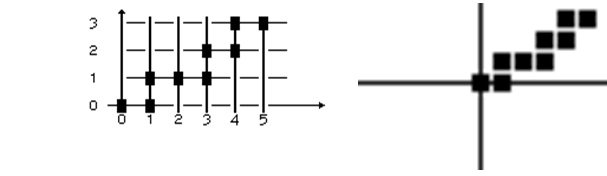Рис. 1. Симметричный ЦДА