Плоская машинная графика, страница 4

Сначала рассмотрим частный случай, когда отрезок прямой принадлежит первой октанте, а затем опишем алгоритм в общем случае и приведем текст программы.

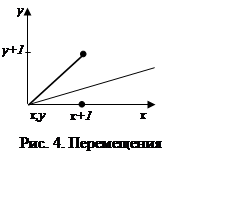Пусть отрезок прямой принадлежит первой октанте плоскости, т. е. Dx>0, Dy>0 и Dx >Dy. Начальная точка (x₀, y₀) принадлежит прямой, следовательно f(x₀,y₀) = 0. Пусть мы сгенерировали некоторую точку (x, y), близкую к идеальной прямой. Так как отрезок принадлежит первой октанте, то из этой точки мы можем перейти либо в точку (x+1, y), либо в точку (x+1, y+1) (рис. 4). При этом f(x+1, y)>0, а f(x+1, y+1)<0. Следовательно, если f(x, y)<0, то переходим в точку (x+1, y), для которой f(x+1, y)>0,  и наоборот, если f(x, y)≥0, то переходим в точку (x+1, y+1), для которой f(x+1, y+1)<0.

Для уменьшения времени работы программы вычислим значения приращений delta1 и delta2:

delta1 = f(x+1, y) – f(x, y) = Dy(x+1-x₀) - Dx(y-y₀) - Dy(x-x₀) + Dx(y-y₀) = Dy > 0,

delta2 = f(x+1, y+1) – f(x, y) = Dy(x+1-x₀) - Dx(y+1-y₀) - Dy(x-x₀) + Dx(y-y₀) =

Dy-Dx <0.

Приращение delta1 положительно, т.к. Dy >0, приращение delta2 отрицательно, т.к. Dx >0, Dy >0, Dx >Dy для первой октанты. Отметим, что независимо от того, в какую точку мы переходим (в (x+1, y) или в (x+1, y+1)), координата xувеличивается на единицу.

Запишем алгоритм:

x, y, Dx, Dy, delta, delta1, delta2 - целые

x = x₀, y = y₀// начальная точка (x₀, y₀)

Dx = x₁ – x₀, Dy = y₁ – y₀

delta = 0, delta1 = Dy, delta2 = Dy - Dx

while (x ≠ x₁ & y ≠ y₁)               // пока не придем в точку (x₁, y₁)

point (x,y)                   // ставим точку с координатами (x, y)

if (delta < 0)

delta = delta + delta1            // положительное приращение

else

delta = delta + delta2            // отрицательное приращение

y = y+1           // y увеличивается на 1

endif-else

x = x+1                       // x увеличивается на 1

endwhile

Сформулируем алгоритм метода приращений для общего случая. Запишем уравнение прямой, проходящей через точки (x₀, y₀) и (x₁, y₁), как f(x,y)= Dy(x-x₀) - Dx(y-y₀)=0 , где Dx = x₁-x₀ иDy=y₁-y₀. Для всякой точки, лежащей справа от направленного отрезка, соединяющего точки (x₀,y₀) и (x₁,y₁), выполнено неравенство f(x,y) > 0. Если точка (x,y) лежит слева, то f(x,y) < 0. Алгоритм генерации точек методом приращений заключается в следующем. Сначала обрабатываются случаи, когда Dx = 0, либо Dy = 0, либо |Dx| = |Dy|. Затем, в предположении, что ни одно из этих условий не выполнено, выбираются два направления движения точки: первое направление параллельно одной из координатных осей и равно (sign(Dx), 0), если |Dx| > |Dy|, и (0, sign(Dy)), если |Dx| < |Dy|; второе направление равно (sign(Dx), sign(Dy)). Если генерируемая точка перемещается во втором направлении, то функция f(x,y) получает приращение ¶₂ f(x,y) = (Dy)sign(Dx) - (Dx)sign(Dy), знак которого не зависит от точки (x,y). Если |Dx| > |Dy|, то при перемещении точки в первом направлении приращение будет равно ¶₁ f(x,y) = (Dy)sign(Dx). Если |Dx| < |Dy|, - то ¶₁ f(x,y) = -(Dx)sign(Dy). Во всех случаях приращения ¶₁f(x,y) и ¶₂f(x,y) имеют противоположные знаки. Стало быть, если текущая точка находится справа от отрезка, то ее следует переместить в том направлении 1 или 2, при котором приращение функции f(x,y) отрицательно, а если слева, то выбирается оставшееся из двух направление. Рассмотрим пример реализации данного алгоритма:

Программа

#include <stdio.h>

#include <conio.h>

#include <graphics.h>

#include <math.h>

int x0, y0 , hx=3, hy=3;

//Функция определения знака целого числа

int sign (int r)

{

if (r>0) return 1;

else if (r<0) return -1;