Опишем этот алгоритм подробнее. Для его реализации нужно знать или уметь вычислять координаты всех точек границы многоугольника. Это является существенным недостатком алгоритма. Многоугольник будем обходить против часовой стрелки. В качестве начальной точки (x0,y0) выбирается вершина многоугольника, имеющая наименьшую координату по Y. Если таких вершин несколько, то из них выбирается вершина с наибольшей координатой по X.
Зная начальную точку (x0,y0) и направление обхода границы многоугольника, вычисляем координаты следующей точки (x1,y1).Точку (x1,y1) назовем текущей точкой (xтек, yтек). Сравним текущую точку (xтек, yтек) и предыдущую точку (xпред, yпред). Возможны три случая:
· yтек > yпред в этом случае xпред заносим в стек и переходим к следующей точке границы многоугольника;
· yтек = yпред в этом случае переходим к следующей точке границы многоугольника;
· yтек < yпред в этом случае извлекаем одно число из стека xстек и проводим горизонтальный отрезок прямой, соединяющий точки (xстек, yтек) и (xтек, yтек), затем переходим к следующей точке границы.
Заполнение закончено, когда просмотрены все стороны многоугольника.
Замечание. Алгоритм можно модифицировать таким образом, чтобы заполнение прекращалось, когда стек исчерпан (заполнение происходит до тех пор, пока стек не пуст). Отметим, что границу многоугольника можно обходить и по часовой стрелке.
Пример 2.1. Построение границы многоугольника с использованием алгоритма Брезенхема и закраски многоугольника с использованием алгоритма с запоминанием точек границы в стек.
Программа
#include <stdio.h>
#include <math.h>
#include <conio.h>
#include <graphics.h>
#define pop() stx[--deep]
#define push(x) stx[deep++]=x
void horline (int y, int x0, int x1)
{
int i;
if (x0>x1) {i=x1; x1=x0; x0=i;}
for (i=x0; i<=x1; i++) putpixel(i, y,15 );
}
void fl(int *arx, int *ary, int dimar)
{
int deep=0;
int stx[1000];
int i0, iglob, ix0, iy0, ix1, iy1;
int ymin;
int ix, iy, deltax , deltay, esh, sx, sy;
int temp, swab, i;
//Находим наименьший ary[i]
i0=0; ymin=ary[0];
for (i=0;i<dimar;i++)
if (ary[i]<ymin) {i0=i; ymin=ary[i];}
//на отрезке (i, i+1) проводим прямую линию от
//arx[i], ary[i] до arx[i+1], ary[i+1]
iglob=i0;
do
{
ix0=arx[iglob]; iy0=ary[iglob];
iglob++; if (iglob==dimar) iglob=0;
ix1=arx[iglob]; iy1=ary[iglob];
//Основной цикл - вывод отрезка по алгоритму Брезенхема
ix=ix0; iy=iy0;
deltax=abs(ix1-ix0);
deltay=abs(iy1-iy0);
if (ix1-ix0>=0) sx=1;
else sx=-1;
if (iy1-iy0>=0) sy=1;
else sy = -1;
if (deltay>deltax)
{
temp=deltax;
deltax=deltay;
deltay=temp;
swab=1;
}
else
swab = 0;
esh=2*deltay-deltax;
for (i=1;i<=deltax;i++)
{
while (esh>=0)
{
if (swab==1) ix = ix + sx;
else
{
iy=iy+sy;
if (sy==1) push (ix);
if (sy==-1)
{
temp=pop();
horline(iy,ix,temp);
}
}
esh=esh-2*deltax;
}
if (swab==1)
{
iy=iy+sy;
if (sy==1) push(ix);
if (sy==-1)
{
temp=pop();
horline(iy,ix,temp);
}
}
else ix=ix+sx;
esh=esh+2*deltay;
}
}
while (i0!=iglob);
}
void main()
{
int gd=VGA, gm=VGAHI;
int arx[3]={600,300,100};
int ary[3]={390,450,120};
initgraph (&gd, &gm, "");
fl(arx,ary,3);
getch(); closegraph() ;
}
Алгоритм, использующий режим вывода прямых XOR_PUT. Этот алгоритм является одним из самых эффектных алгоритмов заполнения. Сначала закрашивается область, большая чем нужно, а затем «лишнее» аккуратно «стирается» (рис. 7).
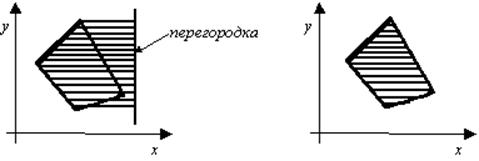
Рис. 7. Алгоритм заполнения с установкой режима XOR_PUT
Осуществляется это с помощью режима XOR_PUT. После вызова функции setwritemode(XOR_PUT) для каждой генерируемой точки отрезка цвет отрезка складывается побитно по модулю 2 с цветом соответствующего пиксела экрана, и результат служит новым цветом этого пиксела. Таким образом, если после установки режима XOR_PUT на экран вывести два раза один и тот же отрезок любого цвета, то в результате сначала отрезок выведется на экран, а потом «сотрется».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.