Плоская машинная графика, страница 5

else return 0;

}

//Функция вывода крупного пиксела

void point (int ix, int iy)

{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1, x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}

//Генерация точек прямой методом приращений

void lineg (int x0, int y0, int x1, int y1)

{

int x=x0, y=y0;

int dx=x1-x0, dy=y1-y0;

int delta=0, ex=sign(dx), ey=sign(dy);

point (x,y);

//Если dx = 0, то выводится вертикальный отрезок

if (dx==0)

{while (y!=y1) point (x, ++y); return;}

//Если dy = 0, то выводится горизонтальный отрезок

if (dy==0)

{while (x!=x1) point (++x, y); return;}

//Если abs(dx) = abs(dy):

if (abs(dx)==abs(dy))

{

while (x!=x1) {x+=ex; y+=ey; point(x,y);}

return;

}

//Основной цикл

while (!(x==x1 && y==y1))

{

if (delta<=0)

{

if (dy*ex-dx*ey>0)

{

x+=ex; y+=ey; delta+=dy*ex-dx*ey;

point(x,y);

}

else

if (abs(dx)>abs(dy))

{

x+=ex; delta+=dy*ex;

point(x,y) ;

}

else

{

y+=ey; delta -=dx*ey;

point(x,y);

}

}

else

{

if (dy*ex-dx*ey<0)

{

x+=ex; y+=ey; delta+=dy*ex-dx*ey;

point(x,y);

}

else

if (abs(dx)>abs(dy))

{

x+=ex; delta+=dy*ex;

point(x,y);

}

else

{

y+=ey; delta-=dx*ey;

point(x,y) ;

}

}

}

}

void main()

{

int gdriver=DETECT, gmode;

initgraph(&gdriver, &gmode, "");

x0=getmaxx()/2; y0=getmaxy()/2;

moveto(0,y0); linerel(getmaxx(),0);

moveto(x0,0); linerel(0, getmaxy());

line4(0,0,5,3);

getch();

closegraph();

}

Точки, выведенные на экран (рис. 5), отличаются от точек, генерируемых с помощью симметричного ЦДА.

 

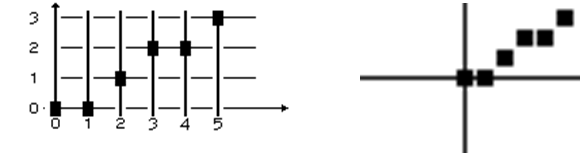Рис. 5. Метод приращений

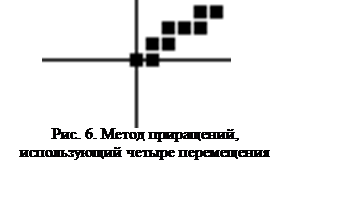Метод приращений, использующий четыре перемещения.

Алгоритм генерации точек прямой по методу приращений можно модифицировать следующим образом: выбор двух направлений перемещения точки производится не из восьми возможных направлений, а из четырех. Разрешается выбирать одно из вертикальных и одно из горизонтальных направлений перемещения точки.

Программа

//Метод приращений использующий четыре перемещения

#include<conio.h>

#include<graphics.h>

#include<math.h>

int x0, y0; //Координаты центра системы координат относит. лев. верх. угла

int hx=3, hy=3; //1/2 ширины и длины пиксела

//Вывод "крупного" пиксела на экран

void point(int ix, int iy)

{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1,x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}

//Функция вывода отрезка по методу

//приращений использующий четыре перемещения

void line4(int x0, int y0, int x1, int y1)

{

int dx=abs(x1-x0), dy=abs(y1-y0);

int ex, ey;

if (x1>x0) ex=1; else ex=-1;

if (y1>y0) ey=1; else ey=-1;

int E=0, x=x0, y=y0;

while((y!=y1) || (x!=x1))

{

point(x,y);

if (E>0) {E-=dx; y+=ey;} else {E+=dy; x+=ex;}

}

point(x,y);

}

void main()

{

int gdriver=DETECT, gmode;

initgraph (&gdriver, &gmode, "");

x0=getmaxx()/2; y0=getmaxy()/2;

moveto(0,y0); linerel(getmaxx(),0);  //Вывод осей координат

moveto(x0,0); linerel(0, getmaxy());

line4(0,0,5,3);         //Вывод отрезка

getch();                //Ожидание нажатия клавиши

closegraph();           //Выключение графического режима

}

Результаты работы программы приведены на рис. 6.

2.2. АЛГОРИТМЫ ЗАПОЛНЕНИЯ

Алгоритм с запоминанием точек границы в стек. Этот алгоритм предназначен для генерации точек выпуклого многоугольника. Определим отношение "<" (лексикографического) порядка на множестве точек плоскости следующим образом: (x,y) < (x',y'), если y < y' или y = y' и x > x'. Будем обходить против часовой стрелки точки границы многоугольника, начиная с вершины многоугольника, наименьшей среди всех его вершин относительно введенного отношения порядка. При увеличении значения ординаты точки, координаты предыдущей точки запоминаются в стек. Если же ордината Y уменьшилась, то извлекается точка из стека и соединяется с текущей точкой. Поскольку величина Y изменяется на ±1, достаточно хранить в стеке только координату X. Ниже мы рассмотрим реализацию, при которой стек представляется в виде массива (пример 2.1).