Плоская машинная графика, страница 2

2) Простой ЦДА. В простом ЦДА e = 1/max{|x₁-x₀|, |y₁-y₀|}. В этом случае либо e×(x₁-x₀), либо e×(y₁-y₀) по модулю равно 1, поэтому для хранения дробной части можно обойтись одним аккумулятором. Положим l = max{|x₁-x₀|, |y₁-y₀|}. Приращения по x и y будут равны dx = (x₁-x₀)/l и dy = (y₁-y₀)/l. Координаты точек, генерируемых простым ЦДА, будут принимать значения

 

X = (int)(0.5 + x₀ + i×dx ),

Y = (int)(0.5 + y₀ + i×dy ),

где i = 0,1,...,l.

Программа

//Метод простого ЦДА

#include<conio.h>

#include<graphics.h>

#include<math.h>

int x0, y0; //Координаты центра системы координат относит. лев. верх. угла

int hx=3, hy=3; //1/2 ширины и длины пиксела

//Функция определения знака целого числа

sign(int r)

{

if(r>0) return 1;

else if(r<0) return -1;

else return 0;

}

//Вывод "крупного" пиксела на экран

void point(int ix, int iy)

{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1,x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}

//Генерация и вывод точек отрезка

void line_cda(int x0,int y0,int x1,int y1)

{

int i,l,x,y;

if(abs(x1-x0)>abs(y1-y0)) l=abs(x1-x0);

else l=abs(y1-y0);

if(l==0) {point(x0,y0); return;}

float hhx=1, hhy=1;

float dx=(float)((x1-x0)/float(l));

float dy=(float)((y1-y0)/float(l));

int ex=sign(x1-x0), ey=sign(y1-y0);

float rez=0.5;          //аккумулятор

x=x0; y=y0;

int flagx=0, flagy=0;   //флаги для проверки на конечную точку

do

{

if(abs(dx)<abs(dy))

{

//приращение всегда по у, а по х при условии rez<=0 rez>=1

point(x,y);

rez+=dx;

if(rez>=1||rez<=0)

{

x+=ex*hhx;

rez-=ex;

}

if(!flagx) flagx=x==x1?1:0;

y+=ey*hhy;

if(!flagy) flagy=y==y1?1:0;

}

else

{

//всегда по х, а по у при условии rez<=0 rez>=1

point(x,y);

x+=ex*hhx;

if(!flagx)flagx=x==x1?1:0;

rez+=dy;

if(rez>=1||rez<=0) {y+=ey*hhy; rez-=ey;}

if(!flagy)flagy=y==y1?1:0;

}

}

while(!(flagx==1 && flagy==1));

point(x1,y1);     //последняя точка

}

void main()

{

int gdriver=DETECT, gmode;

initgraph (&gdriver, &gmode, "");

x0=getmaxx()/2; y0=getmaxy()/2;

moveto(0,y0); linerel(getmaxx(),0);

moveto(x0,0); linerel(0, getmaxy());

line_cda(0,0,5,3);      //Вывод отрезка

getch();                //Ожидание нажатия клавиши

closegraph();           //Выключение графического режима

}

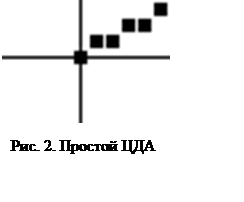
Результаты работы программы приведены на рис. 2.

Алгоритм Брезенхема. Положим Dx = x₁-x₀, Dy = y₁-y₀ . Пусть 0 £Dy £Dx. При изменении координаты x на 1 координата y увеличивается на величину Dy/Dx. Пусть (x, y) - точка пересечения идеальной прямой, проходящей через точки (x₀,y₀) и (x₁,y₁), с прямой x=X, где  (X,Y)  - координаты текущей выведенной точки. Положим d = y-Y. Будем в цикле производить следующие действия: ставим точку и увеличиваем X на 1. При этом величине d придадим приращение Dy/Dx. Если число d вышло из диапазона

-1/2 £ d < 1/2 , то надо координату Y увеличить на 1, а число d уменьшить на 1. Затем переходим к началу цикла. Цикл повторяется Dx + 1 раз. Например, при Dx=4, Dy=1 величина d будет принимать значения 0, 1/4, -1/2, -1/4, 0, в этом случае при x₀ = y₀ = 0 будет сгенерирована последовательность точек – (0,0), (1,0), (2,1), (3,1), (4,1).

Пусть point(x,y) - функция изображения точки. Вводя переменную

e = d-1/2, -1 £ e < 0, приходим к такому алгоритму

X, Y, Dx, Dy - целые

e - вещественное

X = x₀, Y = y₀

Dx = x₁-x₀, Dy = y₁ -y₀(0£Dy£Dx)

e = -1/2

for i = 0 to Dx

point(X,Y)

X = X + 1

e = e + Dy/Dx

while (e ³ 0)

Y = Y + 1

e = e - 1

end while

next i

finish

В отличие от стандартных вариантов, данная версия генерирует и последнюю точку (x₁ ,y₁). Полагая E = 2×Dx×e, приходим к целочисленному алгоритму Брезенхема генерации точек отрезка (при условии 0 £Dy £Dx):

X, Y, Dx, Dy, E - целые