Плоская машинная графика, страница 3

X = x₀, Y = y₀

Dx = x₁–x₀, Dy = y₁-y₀

E = -Dx

for i = 0 to Dx

point(X,Y)

X = X + 1

E = E + 2×Dy

while(E ³ 0)

Y = Y + 1

E = E - 2*Dx

end while

next i

finish

Если (Dx,Dy) принадлежат не первой октанте, то точки (X,Y) генерируются симметрично. Подробнее, пусть x₀, y₀, x₁, y₁ - произвольные целые числа. Тогда, если |Dx| ³ |Dy| , то вектор (Dx,Dy)  находится в одной из октант I, IV, V, VIII. В этом случае координата X генерируемой точки получает на каждом шаге приращение sign(Dx). Если же |Dx| < |Dy|, то надо придавать приращение sign(Dy) координате Y. Приходим к окончательной версии алгоритма Брезенхема.

x₀, y₀, x₁, y₁ - входные параметры, целые

X, Y, dX, dY, E, sx, sy, temp, swap, i - целые

dX = |x₁-x₀|, dY = |y₁-y₀|

sx = sign(x₁-x₀) , sy = sign(y₁-y₀)

if dY > dX (если направление Y - главное)

temp = dX, dX=dY, dY=temp - переставить dX и dY

swab = 1 - была перестановка

else swab = 0

end if-else

E = -dX

for i = 0 to dX

point(X,Y)

E = E + 2×dY

while (E ³ 0)

if (swab = 1) X = X + sx

else Y = Y + sy

end if-else

E = E – 2×dX

end while

if (swab = 1) Y = Y + sy

else X = X + sx

end if-else

next i

finish

Пример программной реализации алгоритма Брезенхема приводится также в     пп. 2.2 (пример 2.1).

Программа

//Метод Брезенхема

#include <conio.h>

#include <graphics.h>

#include <math.h>

int x0, y0; //Координаты центра системы координат относит. лев. верх. угла

int hx=3, hy=3; //1/2 ширины и длины пиксела

//Вывод "крупного" пиксела на экран

void point(int ix, int iy)

{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1,x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}

//Функция вывода отрезка по алгоритму Брезенхема

void bresenham(int ix0, int iy0, int ix1, int iy1)

{

int ix, iy, delta_x, delta_y, esh, sx, sy;

int register temp, swab, i;

ix=ix0; iy=iy0;

delta_x=abs(ix1-ix0); delta_y=abs(iy1-iy0);

if (ix1-ix0>=0) sx=1; else sx=-1;

if (iy1-iy0>=0) sy=1; else sy=-1;

if (ix1==ix0) sx=0;

if (iy1==iy0) sy=0;

//Обмен значений delta_x delta_y в зависимости от угла

if (delta_y > delta_x)

{

temp=delta_x;

delta_x=delta_y;

delta_y=temp;

swab=1;

}

else swab=0;

//Инициализация Е с поправкой на половину пиксела

esh=2*delta_y-delta_x;

for(i=0;i<=delta_x;i++)

{

point(ix,iy);

while(esh>=0)

{

if (swab==1) ix=ix+sx; else iy=iy+sy;

esh=esh-2*delta_x;

}

if (swab==1)iy=iy+sy; else ix=ix+sx;

esh=esh+2*delta_y;

}

}

void main()

{

int gdriver=DETECT, gmode;

initgraph (&gdriver, &gmode, "");

x0=getmaxx()/2; y0=getmaxy()/2;

moveto(0,y0); linerel(getmaxx(),0); //Вывод осей координат

moveto(x0,0); linerel(0, getmaxy());

bresenham(0,0,5,3);     //Вывод отрезка

getch();                //Ожидание нажатия клавиши

closegraph();           //Выключение графического режима

}

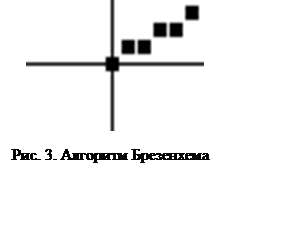
Результаты работы программы приведены на рис. 3.

Примечание. Для улучшения качества изображения применяются алгоритмы сглаживания лестничного эффекта. Точки, находящиеся дальше от прямой, выводятся с меньшей интенсивностью, чем те, которые находятся на прямой. В алгоритме Брезенхема в качестве меры удаленности может быть принят параметр E.

Метод приращений. В пп. 2.3 мы рассмотрим метод приращений для генерации точек кривой. Метод приращений также можно применить и для генерации точек прямой.

Запишем уравнение прямой, проходящей через точки (x₀, y₀) и (x₁, y₁), в виде f(x,y)= 0, а именно: f(x,y)=Dy(x-x₀) - Dx(y-y₀) = 0, где Dx = x₁-x₀ и Dy=y₁-y₀. Все точки области, содержащей отрезок прямой f(x,y)= 0, можно разбить на три множества: множество точек, принадлежащих прямой (для этих точек выполняется условие f(x,y)= 0), множество точек, расположенных справа от прямой (для них выполнено условие f(x,y) > 0), и множество точек, расположенных слева от прямой (для них выполнено условие f(x,y) < 0). Основную идею метода приращений можно сформулировать следующим образом. Если мы выставили точку слева от прямой, то мы стремимся перейти на правую сторону от прямой и наоборот.