Плоская машинная графика, страница 12

Вычислим соответствующие приращения функции f(х,у)

f(х,у₊₁) - f(х,у)      = b²x²+a²(y+1)²-a²b²-b²x²-a²y²+a²b² = a²(2y+1) > 0,

f(х-1,у+1) - f(х,у) = b²(x-1)²+a²(y+1)²-a²b²-b²x²-a²y²+a²b² = b²(-2x+1)+a²(2y+1) < 0.

Первое приращение положительно, так как y>0, а второе приращение отрицательно, так как b²x > a²x для этого отрезка кривой.

Обозначим a² через a2 и b² через b2, запишем алгоритм:

a2=a², b2=b², x=a, y=0, delta=0        //входные параметры

while (b2*x > a2*y)     //пока вектор касательной принадлежит третьей октанте

point(x,y)                                            //ставим точку с координатами (x,y)

if (delta<0)

delta=delta+a2*(y*2+1)       //положительное приращение

else

delta=delta+a2*(y*2+1)+b2(-x*2+1)         //отрицательное приращение

x=x-1                                      // x уменьшается на 1

end if_else

y=y+1                                                 // y увеличивается на 1

end while

Для второго отрезка эллипса вектор касательной V принадлежит четвертой октанте. В этом случае (рис. 14) выполняется условие ½V_y½<½V_x½ и V_y ³ 0.

Первое условие после выполнения цикла while (b2*x > a2*y) выполнено, следовательно, второе условие (V_y ³ 0) определяет принадлежность вектора V к четвертой октанте. Точнее, выполнение этого условия гарантирует, что вектор касательной принадлежит четвертой, а не пятой октанте. Так как V_y=2b²x, то это условие запишется следующим образом: 2b²x³0, упрощая, получим: x³0. Так как вектор касательной принадлежит четвертой октанте (рис. 14), то возможны перемещения

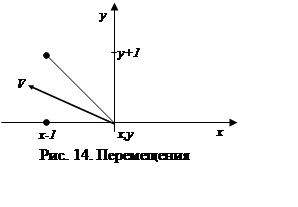
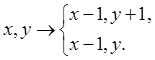
У этих двух перемещений x координата одинакова, следовательно, x уменьшается на 1, независимо от того в какую точку мы будем перемещаться.

Вычислим соответствующие приращения функции f(x,y).           

f(х-1,у+1)= b²(-2x+1)+a²(2y+1)>0,

f(х-1,у) - f(х,у) = b²(x-1)²+a²y²-a²b²-b²x²-a²y²+a²b² = b²(-2x+1) < 0.

Первое приращение положительно, так как b²x < a²y для этого отрезка кривой, а второе приращение отрицательно, так как x³0.

Запишем алгоритм:

while (x³0)                                //пока вектор касательной в четвертой октанте

point(x,y)                                            //ставим точку с координатами (x,y)

if (delta³0)

delta=delta+b2*(-x*2+1)     //отрицательное приращение

else

delta=delta+b2*(-x*2+1)+a2(y*2+1)         //положительное приращение

y=y+1                                     //y увеличивается на 1

end if_else

x=x-1                                                  //x уменьшается на 1

end while

Приведем пример текста программы и результаты ее работы для случая, когда элементом изображения является заполненный прямоугольник, построенный с помощью функции bar.

Программа

#include <graphics.h>

#include <conio.h>

int x0, y0; //экранные координаты начала координат

int hx, hy; //половины ширины и высоты пиксела

void point(int ix, int iy)

{bar (x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1, x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}

void main()

{

int gdriver = DETECT, gmode;

int x, y, a=30, b=20;

float delta;

long a2, b2;

hx=3; hy=3;

//Инициализация графического режима

initgraph ( &gdriver, &gmode, "") ;

x0 = getmaxx()/2; y0 = getmaxy()/2;

moveto(0,y0); linerel(getmaxx(),0);

moveto(x0,0); linerel(0, getmaxy());

a2=a*a; b2=b*b;

x=a; y=0; delta=0;            //начальная точка (x₀,y₀))

while (b2*x>a2*y)             //пока вектор касательной принадлежит третьей

{                       //октанте

point(x,y);             //ставим точку с координатами (x,y)

if (delta<0)

delta+=a2*(y*2+1);//положительное приращение

else

{                 //отрицательное приращение

delta+=a2*(y*2+1)+b2*(-x*2+1);

x--;              //x уменьшается на 1

}

y++;                    //y увеличивается на 1

}

while (x>= 0)                 //пока вектор касательной принадлежит

{                       //четвертой октанте

point(x, y);            //ставим точку с координатами (x,y)

if (delta>=0)

delta += b2*( -x*2 + 1 ); //отрицательное приращение

else

{                 //положительное приращение

delta+=a2*(y*2+1)+b2*(-x*2+1);

y++;

}                 //y увеличивается на 1

x--;                    //x уменьшается на 1

}

getch();

closegraph();                 //выход из графического режима

}

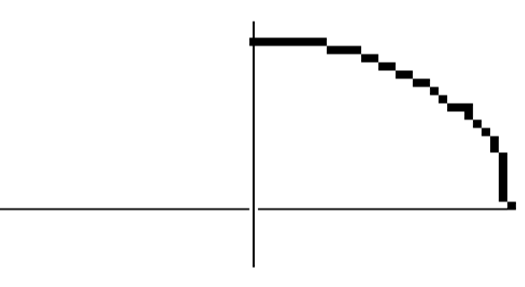
Результат работы программы