Плоская машинная графика, страница 11

В дальнейшем будем руководствоваться следующим правилом. Если методом приращений найдена некоторая точка (x_i,y_i), причем f(x_i,y_i)<0, то для того, чтобы сгенерированная последовательность точек была близка к идеальной кривой, будем стремиться перейти в такую точку (x_i+1,y_i+1), для которой выполняется условие f(x_i+1,y_i+1)>0, и наоборот. Другими словами, если мы выставили точку слева от кривой, то мы стремимся перейти на правую сторону от кривой и наоборот.

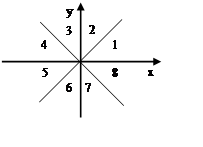
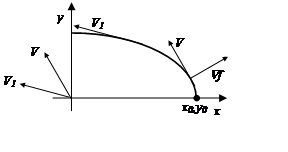
Опишем метод подробнее. Выбираем начальную точку (x₀,y₀), принадлежащую кривой, и направление движения вдоль кривой. Затем разобьем кривую на отрезки кривой, причем для каждого отрезка будет выполняться следующее условие: вектор касательной для всех точек отрезка кривой принадлежит только одной октанте (октанта – это одна восьмая часть плоскости, на рис. 11 приведена нумерация октант). Например, все точки эллипса,  принадлежащие первой четверти, разобьются на два отрезка. Для первого отрезка вектор касательной V принадлежит третьей октанте, а для второго отрезка вектор касательной V₁ принадлежит четвертой октанте (рис. 12).

Рис. 11. Нумерация октант                             Рис. 12. Генерация точек эллипса

Зная уравнение кривой, мы можем найти вектор касательной и определить номер октанты. Для этого сначала запишем градиент

.

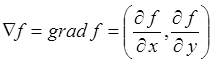Вектор касательной перпендикулярен градиенту (рис. 12). Любому вектору а=(а_х,а_у) на плоскости ОХУ перпендикулярны два вектора: вектор b₁=(-a_y,a_x) и вектор b₂=(a_y,-a_x). Следовательно, градиенту перпендикулярны два вектора

.

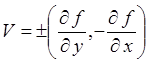Нужный нам вектор определяется, исходя из направления движения вдоль кривой.

Генерацию точек кривой будем производить следующим образом: сначала выведем все точки, принадлежащие первому отрезку кривой, затем второму и т. д. Например, для генерации точек эллипса, принадлежащих первой четверти, требуется вывести два отрезка кривой (рис. 12).

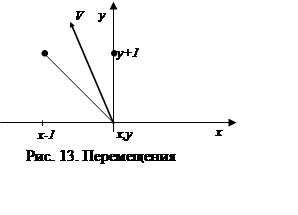
Для всех точек каждого отрезка кривой вектор касательной принадлежит только одной октанте. А зная, какой октанте принадлежит вектор касательной, определим в какие две точки возможно перемещение. Например, если вектор касательной принадлежит третьей октанте (рис. 13), то из точки (х,у) мы можем перейти либо в точку (х,у+1), либо в точку (х-1,у+1).

А для того, чтобы из этих двух возможных точек выбрать одну, воспользуемся сформулированным ранее правилом. То есть из текущей точки (х_i,у_i)  мы можем перейти либо в точку (х_j,у_j), либо в точку (х_k,у_k), причем f(х_j,у_j)×f(х_k,у_k)<0. Пусть f(х_j,у_j)>0, а f(х_k,у_k)<0. В этом случае поступаем следующим образом: если f(х_i,у_i)<0, то переходим в точку (х_j,у_j), и наоборот, если f(х_i,у_i)³0, то переходим в точку (х_k,у_k).

Для уменьшения времени работы программы в дальнейшем, вместо значения f(х_i,у_i) будем вычислять значение величины d_i, причем d_i=f(х_i,у_i). Так как начальная точка (х₀,у₀) принадлежит кривой, то d₀=f(х₀,у₀)=0. Величина d_i вычисляется по формуле

d_i=d_i-1+f(х_i,у_i)-f(х_i-1,у_i-1).

В дальнейшем мы будем вычислять приращение функции f(х,у): f(х_i,у_i)- f(х_i-1,у_i-1).

Пример генерации точек эллипса, принадлежащих первой четверти. Уравнение эллипса х²/а²+у²/b²=1 запишем в виде f(х,у)=b²x²+a²y²-a²b²=0. В качестве начальной точки (х₀,у₀) рекомендуется выбирать точку кривой, принадлежащей оси координат. В нашем случае, в качестве начальной точки можно выбрать точку (а,0) или (0,b). Выбираем точку х₀=а, у₀=0. Направление движения вдоль кривой – против часовой стрелки. Мы уже отмечали (рис. 12), что, в этом случае, сначала выводится отрезок кривой, для которого вектор касательной принадлежит третьей октанте, а затем отрезок, для которого вектор касательной принадлежит четвертой октанте.

Запишем градиент функции f

.

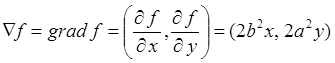Вектор касательной равен либо V=(-2a²y, 2b²x), либо w=(2a²y, -2b²x). Вектор w=(w_x,w_y) принадлежит седьмой октанте (рис. 11), так как w_x>0, а w_y<0. Вектор V=(v_x,v_y) принадлежит третьей октанте (рис. 12), так как V_x<0, a V_y>0. Следовательно, вектор касательной V=(-2a²y, 2b²x).

Запишем условие, при выполнении которого, вектор касательной принадлежит третьей октанте: ½V_y½>½V_x½, в нашем случае: ½2b²x½>½-2a²y½. Учитывая, что x>0 и y>0, так как они принадлежат первой четверти, получаем условие b²x>a²y. Если  вектор касательной принадлежит третьей октанте (рис. 13), то возможны два перемещения

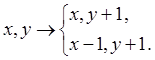
Отметим, что у этих двух перемещений у координата одинакова, следовательно, не зависимо от того в какую точку мы будем перемещаться, у увеличится на 1.