1.7. Оптимальный выбор структуры ГПС в условиях неопределенности
развития производства
При управлении ТП часто возникает необходимость принятия решения в условиях неопределенности. Неопределенность при анализе ТП появляется из-за неполного знания общей физической и статистической природы явлений, происходящих в технологических и социальных системах. В этих случаях необходим математический аппарат, позволяющий принять решения в условиях ограниченной информации и выбрать оптимальные варианты. Подобные задачи в математике анализируются в теории игр и статистических решений [1,2,5] .
Во многих случаях необходимо определить оптимальное поведение по отношению к противодействующей стороне (противника), действие которой случайно. В этом случае возникает конфликтная ситуация, определяющаяся как игра, для которой формируют математическую модель и определяют правила игры, т.е. определяются противодействующие стороны (игроки) и исход конфликта (выигрыш или проигрыш).
Под игрой понимаются мероприятия, состоящие из ряда действий сторон. Если в конфликте участвует две стороны, игра называется парной, если более двух - множественной.
Стратегия игрока определяется как совокупность правил, характеризующих выбор варианта действий при каждом ходе противодействующего игрока в зависимости от сложившейся ситуации. Оптимальная стратегия игрока характеризуется тем, что при многократном повторении игры обеспечивается максимально возможный средний выигрыш (или минимально возможный средний проигрыш), выражаемый в количественной форме.
Модель игры обычно записывается в виде платежной
матрицы. Рассмотрим парную конечную игру, имеющую конечное число стратегий, в
которой игрок А (мы) имеет ![]() , а игрок В (противник)
-
, а игрок В (противник)
- ![]() стратегий. Такую игру называют игрой m x n . Обозначим наши стратегии
стратегий. Такую игру называют игрой m x n . Обозначим наши стратегии ![]() ,
, ![]() ,
, ![]() , … ,
, … , ![]() , а
стратегии противника -
, а
стратегии противника - ![]() ,
, ![]() ,
,
![]() , … ,
, … , ![]() .
.
Пусть каждая сторона выбрала
определенную стратегию ![]() и
и ![]() .
Тогда исход игры (наш выигрыш) обозначим
.
Тогда исход игры (наш выигрыш) обозначим ![]() . Если
игра содержит случайные ходы, то выигрыш при паре стратегий
. Если
игра содержит случайные ходы, то выигрыш при паре стратегий ![]()
![]() будет
случайной величиной, зависящей от исходов всех случайных ходов. Тогда
оценкой ожидаемого выигрыша является математическое ожидание случайного выигрыша.
будет
случайной величиной, зависящей от исходов всех случайных ходов. Тогда
оценкой ожидаемого выигрыша является математическое ожидание случайного выигрыша.
Предположим, что известны ![]() при каждой паре стратегий
при каждой паре стратегий ![]()
![]() ,
тогда можно составить платежную матрицу игры (табл.1)
,
тогда можно составить платежную матрицу игры (табл.1)
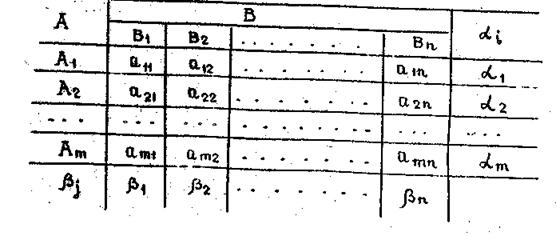
Для принятия решения в такой
игре необходимо выбрать стратегию ![]() , которая давала бы
выигрыш в определенном смысле [8,10] .
, которая давала бы
выигрыш в определенном смысле [8,10] .
Правила принятия решения могут быть статистическими и детерминированными.
Детерминированные правила принятия решений
Правила минимакса (максимина). В этом случае игровая ситуация строится
следующим образом. В качестве результата игры ![]() рассматривается
потери (табл.1) стороны В в соответствующих показателях. Необходимо
определить наибольшие потери для каждого выбора стратегии
рассматривается
потери (табл.1) стороны В в соответствующих показателях. Необходимо
определить наибольшие потери для каждого выбора стратегии ![]() в столбцах платежной матрицы, а
затем сделать выбор, приводящий к минимизации максимальных потерь;
математически это выражается в виде
в столбцах платежной матрицы, а
затем сделать выбор, приводящий к минимизации максимальных потерь;
математически это выражается в виде
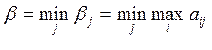 .
.
Эта запись интерпретируется
следующим образом. Для каждого выбора стратегии ![]() определять
наибольшее значение
определять
наибольшее значение ![]() в столбцах платежной
матрицы результата
в столбцах платежной
матрицы результата ![]() , а затем найти такой
выбор
, а затем найти такой
выбор ![]() , который имеет наименьшее значение
из
, который имеет наименьшее значение
из ![]() , т.е.
, т.е. 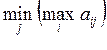 .
.
Аналогично игра со стороны ![]() подразумевает в качестве результата
выигрыш (прибыль). При этом определяются минимальный выигрыш для каждого выбора
стратегии
подразумевает в качестве результата
выигрыш (прибыль). При этом определяются минимальный выигрыш для каждого выбора
стратегии ![]() в строках платежной матрицы, а
затем выбирается такая стратегия
в строках платежной матрицы, а
затем выбирается такая стратегия ![]() , которая приводит
к максимизации минимального выигрыша, т.е.
, которая приводит
к максимизации минимального выигрыша, т.е.
![]() .
.
Это правило иногда называют правилом пессимиста, или правилом консервативного игрока, в том смысле, что игрок при принятии решения желает застраховать себя от высоких потерь.
Правило максимального (минимального) выбора.
Критерий в данном случае записывается следующим образом:
![]() ,
,
если в качестве результата рассматривать прибыль или экономический эффект стороны А , и
![]() ,
,
если рассматривать потери или убытки от выбора той или иной стратегии стороны В . Это правило называет правилом оптимиста, или правилом азартного игрока.
Правило Гурвица. Этот критерий базируется на комбинации максимального и максиминного критериев. Альтернативное действие выбирается в соответствии с выражением
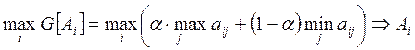 ,
,
где ![]() -
весовой коэффициент критерия. Из этого выражения следует, что при
-
весовой коэффициент критерия. Из этого выражения следует, что при ![]() этот критерий переходит в максиминный
этот критерий переходит в максиминный
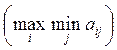 , а при
, а при ![]() -
в максимальный
-
в максимальный 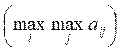 . В связи с этим правило
Гурвица устанавливает компромисс между правилами пессимиста и оптимиста.
. В связи с этим правило
Гурвица устанавливает компромисс между правилами пессимиста и оптимиста.
Правило Лапласа. Правило Лапласа является своеобразным
компромиссом между детерминированными критериями и статистическими правилами
принятия решения. В этом случае используется следующий принцип: если намерения
противостоящей стороны неизвестны и все стратегии ![]() равновероятны,
т.е. нет доказательств, что одна стратегия более вероятна, чем другая, то
стратегии
равновероятны,
т.е. нет доказательств, что одна стратегия более вероятна, чем другая, то
стратегии ![]() (
(![]() ,
, ![]() ,
, ![]() ,
… ,
,
… , ![]() , … ,
, … , ![]() )
оцениваются одинаковыми вероятностями применения
)
оцениваются одинаковыми вероятностями применения
![]()
В этом случае выбор
осуществляется следующим образом. Определяется максимальная ожидаемая оценка
результата при выборе стратегии ![]()
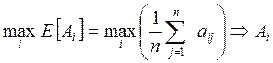 .
.
Статистическое правило принятия решения
В тех случаях, когда точных знаний
об использовании стратегий противником ![]() нет,
тогда проблема выбора стратегии
нет,
тогда проблема выбора стратегии ![]() требует знания
вероятностей
требует знания
вероятностей ![]() (
(![]() ,
,
![]() ,
, ![]() ,
… ,
,
… , ![]() , … ,
, … , ![]() ) применения
стратегий
) применения
стратегий ![]() (
(![]() ,
, ![]() ,
, ![]() ,
… ,
,
… , ![]() , … ,
, … , ![]() ) .
) .
Если каким-либо образом удается определить
эти вероятности, то выбор решения осуществляется в условиях риска. Критерием
выбора решения в данной ситуации является максимум ожидаемого результата при
выборе стратегии ![]() , который выражается следующим
образом
, который выражается следующим
образом
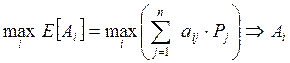 ,
,
где ![]() +
+![]() +
+![]() +… +
+… +![]() +
… +
+
… +![]() = 1.
= 1.
При отсутствии информации о вероятностях применения противником стратегий можно вычислить ожидаемые значения каждого выбора для различных вероятностей и определить границы ожидаемых значений результата для каждого выбора.
Задача выбора вариантов ГПС
В настоящее время разработано множество вариантов ГПС. В каждом конкретном случае необходимо при проектировании выбирать наилучший среди них с точки зрения технических, организационных и экономических решений. При этом следует учитывать следующие условия [2,13].
1. Существует множество альтернативных вариантов ГПС, реализующих в ряде случаев взаимоисключающие друг друга концепции создания ГПС, различные конструктивные и технологические решения и т.д.
2. Возможно существование множества условий, в которых окажется ГПС после соз-дания, включающих условия эксплуатации, конструктивно-технологические особенности изготавливаемых изделий, особенности развития технологии. Указанные условия не могут контролироваться и управляться разработчиком ГПС, они существуют объективно и независимы от его воли.
3. Может быть получено некоторое множество результатов при создании ГПС в различных условиях эксплуатации в зависимости от выбранного альтернативного решения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.