Оптимальный выбор структуры ГПС в условиях неопределенности развития производства, страница 10

2.  Матрицы систем ограничения двойственных задач получаются одна из другой с помощью операции транспонирования.

3.  Неравенства систем ограничений имеют противоположный смысл, при этом в обеих задачах существуют требования положительности переменных.

4.  Свободные члены системы ограничений одной задачи становятся коэффициентами целевой функции двойственной.

5. В одной задаче целевая функция максимизируется, в другой - минимизируется, т.е. экстремумы целевых функций двойственных задач имеют противоположный смысл.

7.5. Задача календарного планирования

Для решения задач календарного планирования наиболее мощным является метод имитационного моделирования, предусматривавший проведение имитационного эксперимента на моделях, структурно подобных моделируемому объекту.                                                                                           

Структурное подобие модели и объекта моделирования существенно упрощает внесение текущих изменений в модель. Этот процесс в производственных условиях может быть организован в форме диалога с oпeратором, который не имеет специальных математических знаний.

Имитационные методы строятся по схеме последовательного анализа вариантов на основе правил предпочтения. Эта схема связана с пошаговым конструированием вариантов с помощью моделирования, в процессе которого имитируется прохождение материальных   потоков через производственный участок. Алгоритм решения задачи отроится следующим образом.

Вычисляется моменты завершения операций на каждой единице оборудования, формируется список всех операций, готовых к выполнению, и возможные варианты закрепления операций за оборудованием. Полученные варианты сравниваются на основе принятых правил предпочтения и выбирается доминирующий вариант. Этот процесс последовательно повторяется до тех пор, пока все операции не будут распределены по оборудованию. При построении имитационной модели сравнительно просто учитываются такие трудноформализуемые в аналитических моделях ограничения, как структура транспортной сети, временный дефицит ресурсов, частичная и временная потеря работоспособности оборудования и ряд других.

Имитационные методы, имеющие эвристический характер, проще с вычислительной точки зрения, но и с их помощью трудно получить оптимальное решение задачи.

8.  НАДЕЖНОСТЬ  ГПС

Гибкая производственная система представляет собой большую, сложную и активную систему, включающую множество разнородных элементов (механические системы ТО, АТНС, складские системы и системы управления всех уровней). В связи с этим проблема надежности ГПС является в настоящее время важнейшей. По данным литературных источников, ГПС должна безотказно работать в течение двух смен, т.е. 16 часов в сутки. Во время третьей смены осуществляется профилактика всего оборудования, загрузка и выгрузка складов, подготовка и ремонт оборудования.

Под надёжностью объекта понимается свойство последнего сохранять свою работоспособность при заданных условиях эксплуатации в течение заданного промежутке времени. Надежность представляет собой комплексную характеристику, включающую свойства безотказности, долговечности, сохраняемости и ремонтопригодности. Не уменьшая важности остальных свойств, рассмотрим важнейшее среди них   - свойство безотказности.          

Все элементы ГПС разделяются на два основных вида - невосстанавливаемые и восстанавливаемые. Невосстанавливаемые элементы, поведение которых существенно лишь до первого отказа, характеризуются интенсивностью отказов, частотой отказов, вероятностью безотказной работы, вероятностью отказа и наработкой на отказ .

Восстанавливаемые элементы, эксплуатация которых допускает многократный ремонт, характеризуются интенсивностью потока отказов ; интенсивностью потока восстановлений ; коэффициентом готовности ; средним временем работы между отказами   и средним временем восстановления.

8.1. Оценка надежности невосстанавливаемых элементов ГПС

Расчет надежности элементов на основе -характеристик

Для невосстанавливаемых элементов вероятность безотказной работы связана с интенсивностью отказов соотношением

  .

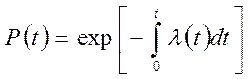Для экспоненциального закона вероятности безотказной работы, т.е.

  ,

а наработка на отказ

   .

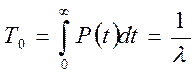Система из невосстанавливаемых элементов, характеризующихся независимыми отказами, имеет интенсивность отказов

        ,

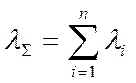где - интенсивность отказов -го элемента; - количество элементов.

            Тогда вероятность безотказной работы

  .

8.2. Оценка надежности восстанавливаемых элементов ГПС

Большинство элементов ГПС является восстанавливаемыми. Для анализа надежности восстанавливаемых систем используют результаты теории массового обслуживания. Основным понятием теории массового обслуживания является поток случайных событий [4] .

Потоком случайных событий называют временной поток событий, происходящих в случайные моменты времени. Для характеристики потоков используют множество вероятностей   происхождения  событий на интервале времени  .   Основные свойства потоков случайных событий

1.  Стационарность. Характеризуется тем, что вероятность появления к событий в интервале времени , расположенном на расстоянии   не зависит от  , а зависит только от длины интервала .

2.  Ординарность. Для ординарного потока вероятность появления двух к более событий в элементарном интервале  есть величина более малого порядка, т.е.

  .

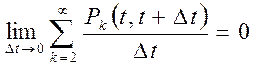3.  Последействие. Поток с последействием - это поток, в котором величины вероятностей зависят от того, сколько событий произошло на интервале  и когда они произошли.                                              

4.  Поток, обладающий свойством стационарности, ординарности и беспоследействия, называется простейшим потоком.

Числовыми характеристиками потоков являются:

- параметр потока

  ,

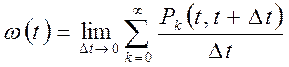и интенсивность потока событий

  .

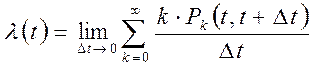Рассмотрим методику анализа надежности на основе теории массового обслуживания, пользуясь простейшим примером.

Основные этапы методики.

1.  Формулирование задачи.

2.  Определение понятий состояний системы. Нумерация состояний.