Оптимальный выбор структуры ГПС в условиях неопределенности развития производства, страница 9

Выбор критерия эффективности осуществляется индивидуально для каждого конкретного производственного подразделения по результатам анализа его экономических, организационных и технических особенностей. Наиболее часто используют следующие критерии эффективности.

1.  Минимизация времени выпуска заданного объема продукции

 ,

где  - множество единиц оборудования; - суммарное время выполнения операций -й единицы оборудования;  и - суммарное время переналадок и простоя -й единицы оборудования.

Иногда используют частные случаи указанного критерия, например

 .

2.  Максимизация загрузки оборудования

 .

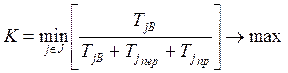При этом объем выпуска продукции считается заданным.

3.  Минимизация суммарных производственных затрат

 .

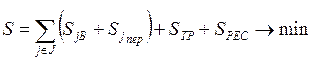где  , - суммарные затраты на выполнение операций и переналадку  -го оборудования; - суммарные затраты на транспортно-складские операций и энергетические ресурсы.

Кроме очевидных ограничений на практике при решении задач календарного планирования приходится учитывать еще ряд других. Рассмотрим некоторые из них, характерные для ГПС.

1. Структура сети транспортных маршрутов. Особенности этой структуры определяет возможности и время транспортировки деталей между оборудованием участка.  Структура транспортной сети должна допускать выполнение всех технологических маршрутов, что является условием работоспособности участка. Характерной для некоторых ГПС является структура типа "передача через склад". При ее использовании после обработки на определенной единице оборудования деталь возвращается на склад и оттуда подается на дальнейшую обработку.

2.         Директивные сроки окончания обработки определенных деталей.
Для ряда деталей внутри планового периода могут быть заданы ограничения типа , где  - директивный срок окончания обработки -й детали.

3.         Ресурсные ограничения. Выполнение заданного множества операций требует расхода определенных материалов, инструментов, энергии, которые в реальном производстве ограничены.

Кроме перечисленных ограничений приходится учитывать емкости накопителей и складов, скорости работ складского оборудования, наличие и готовность управляющих программ.

7.3. Задача определения оптимальной программы выпуска

Положим, существует некоторая ГПС, перед которой стоит задача выпуска продукции определенного ассортимента. Для этого у ГПС есть ресурсы: сырье, материалы, комплектующие, фонды, рабочая сила, энергия и т.д. На каждый ресурс есть ограничения, которые ГПС не имеет права превысить. Также известно, что для производства продукции каждого вида потребуется определенное количество ресурса каждого вида.

Требуется определить, сколько единиц продукции каждого вида должна произвести ГПС, чтобы, с одной стороны, получить максимальную прибыль от реализации продукции, а с другой - максимально использовать все ресурсы, не превысив их.

Рассмотрим эту задачу с точки зрения линейного программирования. Очевидно, что целевой функцией, которую необходимо максимизировать, является прибыль, получаемая ГПС. Неизвестными , , … ,  является количество единиц продукции каждого вида, выпускаемых ГПС,  - номенклатура видов продукции. Коэффициентами функционала (целевой функции) является прибыль, получаемая от продажи единицы каждого вида продукции   , , … ,  .

Соответственно коэффициентами системы ограничений    будет величина   -го ресурса, которая необходима для производства единицы   -го вида продукции. Постоянные , , … ,  определяет ограничения, накладываемые на каждый вид ресурса. Необходимо отметить, что в этой задаче на переменные , , … ,  накладываются ограничения неотрицательности, поскольку решение теряет смысл, если хотя бы одна из переменных принимает отрицательное   значение. Тогда задача определения оптимальной программы выпуска ГПС может быть поставлена следующим образом.

Найти такие значения  , , … ,  количеств выпускаемой продукции, которые бы давали максимум прибыли, получаемой предприятием от продажи выпущенных изделий, т.е.

 ,

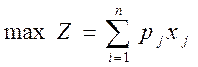при ограничениях на все виды ресурсов

      ,

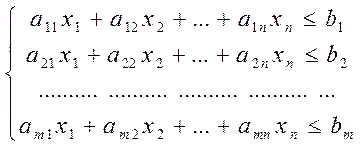учитывая, что .

Таким образом, значения  , , … ,  являются оптимальной программой выпуска изделия ГПС с точки зрения максимальной прибыли производства.

7.4. Задача определения эффективности ГПС

Организация нового производства всегда должна определяться технико-экономической эффективностью. Если предприятие обладает всеми ресурсами, то при организации производства оно должно получить прибыль, в противном случае выгоднее продать эти ресурсы. Тогда задача эффективности ГПС сводится к задаче определения оптимальных цен на ресурсы предприятия.

Допустим, некоторая организация решила закупить все ресурсы предприятия. Необходимо установить оптимальные цены на эти ресурсы  , , … ,     исходя из следующих условий:

-  общая стоимость ресурсов покупающая организация стремится минимизировать;

-  за каждый вид ресурсов предприятию надо заплатить не менее той суммы, которую оно может получить при его переработке в готовую продукцию. В противном случае предприятию выгоднее не продавать ресурсы, а организовать собственное производство.

                Общая стоимость ресурсов W   выразится суммой

  ,

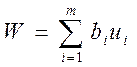которая и будет целевой функцией задачи.

Ограничения этой задачи формулируется из следующих соображений. На единицу продукции первого вида расходуется  единиц первого вида ресурса ценой ,   единиц ресурса второго вида ценой  и т.д.;  единиц ресурса m-го вида ценой . Стоимость всех ресурсов, идущих на производство единицы продукции первого вида, должна быть не менее прибыли от продажи единицы продукции первого вида , т.е.

 .

Аналогично задаются и остальные ограничения. В этом случае задача формулируется следующим образом.

Определить оптимальные значения цен  такие, которые бы минимизировали общую стоимость

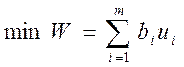
при ограничениях

  .

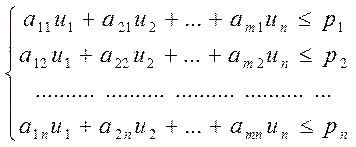
таким образом, если цены на ресурсы будут ниже рассчитанных, то организация ГПС будет эффективна.     

Представленная задача является двойственной по отношению к предыдущей и позволяет выявить основные свойства двойственных задач линейного программирования.

1.  Количество неизвестных одной задачи равно числу неравенств системы ограничений другой.