Оптимальный выбор структуры ГПС в условиях неопределенности развития производства, страница 8

Это обстоятельство дает возможность не испытывать на оптимальность все бесчисленное множество точек многогранника, а ограничиваться только перебором его вершин. Отсюда выявляется способ решения задачи  - определить любую вершину многогранника, а затем от вершины к вершине добираться до нужной точки, т.е. до экстремума.

Для примера рассмотрим решение следующей задачи линейного программирования. Целевая функция задается в виде

 ,

а ограничения

,

,

;.

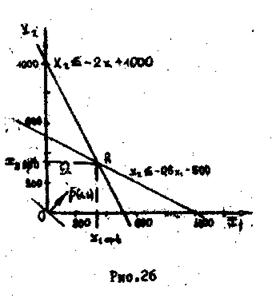
Геометрическая интерпретация этой задачи приведена на рис.26. Вектор градиента Р   целевой функции имеет направляющие проекции [1,1]. Точка R определяет экстремум целевой функции, который достигается при и .

5.3. Транспортная задача

В тех случаях, когда на производстве осуществляется сложные перевозки продукции, т.е. имеется  пунктов отправления (cкладов) с запасами , единиц груза в каждом, и           _пунктов назначения (участков ГПМ и т.д.) с потребностями  , , используют постановку транспортной задачи. При этом предусматривается, что стоимость перевозки единицы продукции по соответствующему маршруту от -го склада   -му потребителю задается матрицей, элементы которой , ;   известны.

Решением задачи при такой постановке будет являться матрица , где - элементы матрицы, определяющие количество единиц продукции, которое необходимо доставить из    -го склада -му потребителю (матрица перевозки).

Формальная постановка задачи сводится к формализации целевой функции и ограничений. В качестве целевой функции в этой задаче можно принять минимум стоимости перевозок по всем пунктам отправления и назначения

  ,

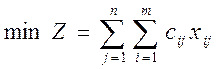при ограничениях на запасы складов

;  ,

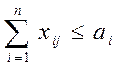и ограничениях на достаточность потребности пунктов назначения

 ;   ,

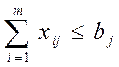и                                                    , .

В том случае, если

 ,

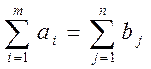транспортная задача называется закрытой, в противоположном   случае - открытой.

7. ОПЕРАТИВНОЕ УПРАВЛЕНИЕ В ГПС

Оперативное управление представляет собой процесс временной и пространственной организации производства. Структурно оперативное управление подразделяется на три группы задач, взаимосвязь между которыми образует иерархическую трехуровневую структуру.

На первом (нижнем) уровне решаются задачи управления отдельными технологическими операциями и их элементами. Как правило, в автоматическом режиме эти функции выполняются регуляторами, являющимися элементами СУ оборудованием.

На втором уровне решаются задачи локального управления оборудованием, основные функции которых заключаются в выполнении последовательности технологических операций в соответствии с заданной программой (логическое управление). Содержание программы управления зависит от типа оборудования, для сборочного центра программой задается последовательность движений робота-сборщика, моменты смены рабочего инструмента и посылки команд на загрузку и разгрузку сборочной позиции объектами оборки. Программа содержит также информацию о значениях технологических параметров операций, которые используется регуляторами первого уровня.

Не третьем уровне решаются задачи управления материальными потоками, проходящими через технологическое подразделение.

Можно выделить две основные задачи оперативного управления: оперативное (календарное) планирование; оперативный контроль и корректировка планов.

Основной характеристикой системы оперативного управления ГПС является скорость реакции на изменение условий функционирования производства. Характерными для ГПС являются отказы оборудования, нестабильность качества исходных материалов и их поставок, смена номенклатуры выпускаемой продукции, изменения режимов функционирования системы, связанные с переналадками оборудования и т.д. Таким образом, система оперативного управления ГПС должна быть гибкой и быстро приспосабливаться к текущим условиям производства.

7.1. Оперативное планирование

Оперативное планирование представляет процесс программирования деятельности всех элементов технологического подразделения в пределах заданного периода времени - планового периода. На этот период технологическому подразделению устанавливается план выпуска продукции по объёму и номенклатуре.  

Результатом решения задачи календарного планирования является временное и пространственное упорядочение комплекса запланированных работ. Временное упорядочение выражается в определении сроков начала и окончания выполнения работ, а пространственное - в назначении работ на определенное ТО.

В автоматизированном варианте результаты планирования оформляются в виде задания, либо представляющего собой комплекс программ, передаваемых в локальные системы управления, либо на программных носителях.

Формально задача планирования ставится следующим образом.

Пусть на технологической участке требуется обработать      деталей (или их партий). Обозначим   операцию с номером  ; , которая выполняется над -й деталью, ;  - число операций, которое необходимо выполнить над -й  деталью;    - номер группы оборудования, настроенного на выполнение операции ;   - номинальная продолжительность выполнения операций .

Последовательность операций или прохождения детали через группы оборудования является технологическим маршрутом

  .

Обозначим    - момент начала,  а  - момент окончания операции . Предположим, что каждая операция выполняется без перерыва, т.е. удовлетворяется соотношение

  .

Очевидным условием является также проведение в каждый момент времени на каждой единице оборудования только одной операции. Совокупность чисел  называется календарным планом.                                         

При формальной постановке задачи календарного планирования требуется задать целевую функции планирования, которая каждому плану  ставит в соответствие некоторое число , оценивающее эффективность плана. Целевую функцию часто называют критерием эффективности. Задача оптимального планирования заключается в отыскании такого плана , который дает экстремум критерия эффективности  и удовлетворяет ограничениям.

7.2. Критерии эффективности оперативного управления ГПС