Оптимальный выбор структуры ГПС в условиях неопределенности развития производства, страница 12

В большинстве случаев бывает достаточным знание предельных вероятностей состояний, характеризующих стационарный режим работы системы (при ). Для этого следует левые части уравнений (производные) положить равными нулю и решить полученную таким образом систему линейных алгебраических уравнений:

                                  ,

  ,

  ,

  ,

  .

Вероятность   будет определять отказ информационной системы по обработке заявок.

8.4. Оценка надежности технологической системы

Технологическая система, реализующая групповую обработку кристаллов микросхем, вносит дефекты на кристаллах. Интенсивность возникновения дефектов на кристаллах одинакова и равна . При возникновении дефекта кристалл отказывает с вероятностью . Определить вероятности состояния системы при прохождении через ТП пластины из 4 кристаллов.

Состояния системы характеризуется количеством бездефектных кристаллов, прошедших через ТП:

 - все кристаллы бездефектны;

- один кристалл отказал, три остались бездефектными;

 - два кристалла отказали, два остались бездефектными;

 - три кристалла отказали, один остался бездефектным;

 - все кристаллу отказали.

Граф состояний системы представлен на рис.38. Для разметки графа определим интенсивности потоков событий, переводящих систему из одного состояния в другое. Из состояния  в  систему переводит поток дефектов. Интенсивность дефектообразования кристаллов  ,  но не все дефекты являются опасными, т.е. приводящими к отказу.

Дефект кристалла является опасным с вероятностью  . Так как система в состоянии  состоит из четырех кристаллов, на каждый из которых действует поток опасных дефектов с интенсивностью , то на систему в целом действует поток опасных дефектов с интенсивностью 4.  Аналогично из состояния  в  система переводится потоком опасных дефектов  3, из  в  - 2 , а из  в - .

Вероятности состояния системы обозначим соответственно   .

Уравнения Колмогорова для вероятностей состояния имеет вид

  ,

  ,

  ,

  ,

  ,

.

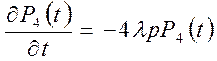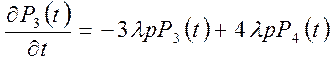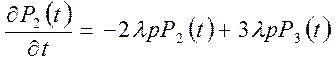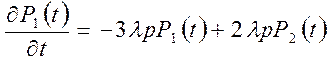Начальные условия задачи при  - все кристаллы бездефектны, т.е. ; .

Судя по графу, данная система является разомкнутой, т.е. из состояния  система не имеет выхода ни в какое другое   состояние. Это говорит о том, что в этой системе   стационарного   режима   быть не может.

8.5. Анализ вероятностных характеристик транспортной системы

Транспортная система, переводя заготовки со склада к ТО, paзгружает их и загружает готовые изделия, которые опять перевозит на склад. Состояния системы можно определить следующим образом:

 - загрузка заготовок на складе;

- разгрузка заготовок на ТО;

- загрузка готовых изделий на ТО;

- разгрузка готовых изделий на складе.

В этом случае состояния системы связаны в кольцо (цикл) с односторонними переходами (рис.39), интенсивности которых - ₁ , 2 ,3 ,4  .   Поэтому процесс, протекающий в такой системе, называется циклическим. Задача состоит в определении предельных вероятностей состояний системы, считая, что время перевозки намного меньше времени   загрузки.

Составим систему уравнений Колмогорова для вероятностей состояний

  ,

  ,

  ,

  ,

.

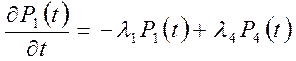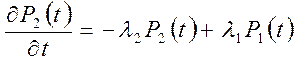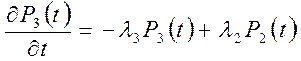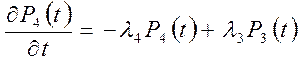Приравняв нулю левые части уравнений, получим алгебраические уравнения для предельных вероятностей состояний

, , ,  ,

решение которых при нормировочном уравнении даст аналитические выражения

,  , , .

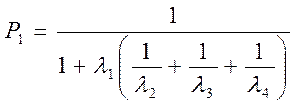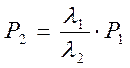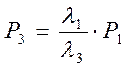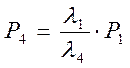Если заданы средние времена пребывания системы  в состояниях  , ,  , … , соответственно ,,, … ,, то предельные вероятности состояний в циклической схеме

  ,

  ,

……………………………………

  ,

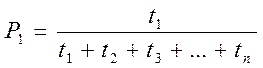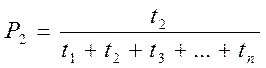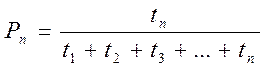или в общем случае

  .

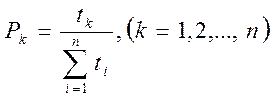Полученные предельные вероятности  дают возможность рассчитать основные организационно-технологические характеристики рассматриваемой транспортной системы.

Библиографичеокий описок

1.  Абчук В.А., Матвейчук Ф.А., Томашевскнй Л.П. Справочник по исследованию операций. М.: Воениздат, 1979. 368 с.    

2.  Гаспаров Д.В., Дахнович А.А. Оптимизация технологических процессов в производстве электронных устройств: Учеб.пособие для вузов. М.: Высш. шк., 1986. 191 с.

3.  Гибкое автоматическое производство/Под ред. С.А.Майорова, Г.В.Орловокого. Л.: Машиностроение, 1983. 376 с.

4.  Горячев A.B. Шишкевич А.А. Микропроцессоры. Информаиионно-управляющие вычислительные системы: Учеб. пособие для вузов /Под ред. Л.Н. Преснухина. М.: Высш. шк., 1984. 120 с.

5.  Карлин С. Математические методы в теории игр, программировании и экономике: Пер. с англ. М.: Мир. 1964. 286 с.

6.  Козырев Ю.Г. Промышленные роботы: Справочник. М.: Машиностроение, 1983. 376 с.

7. Ларичев О.И. Проблемы взаимодействия человек-ЭВМ в системах поддержки принятия решений//Процедуры оценивания многокритериальных объектов: Сб.ст./ВНИИСИ. М., 1984. С.20-28.

8.  Лефевр В.А., Смолян Г.Л. Алгебра конфликта. М.: Знание, 1968. 176 с.

9.  Логашов В.Г. Технологические основы ГАП. Л.: Машиностроение, 1985. 175 с.

10. Мак-Кинси Д. Введение в теорию игр: Пер. с англ. М.: Физматгиз, I960. 340 с.

11. Митрофанов С.П. Групповая технология в машиностроительном
производстве: В 2 т. Л.: Машиностроение, 1983. T.1. 360 с. Т.2.376 с.

12.Морозов В.П., Дынарский Я.С. Элементы теории управления ГАП: Математическое обеспечение. Л.: Машиностроение, 1984. 333 с.

13. Нейман Д., Моргенштерн Ф. Теория игр и экономическое поведение: Пер. с англ. М.: Мир. 1970. 287 с.

14. Разработка САПР: В 10 кн. Кн.8. Математические методы анализа производительности и надежности САПР: Практ.пособие/В.И.Кузовлев, П.Ч.Шкатов; Под ред. А.В.Петрова. М.: Высш.шк.. 1990. 144 с.

15.Робототехника и гибкие автоматизированные производства: В 9 кн. Кн.1. Системные принципы создания гибких автоматизированных производств: Учеб.пособие для втузов/И.М.Макаров. М.: Высш.шк. 1986. 175 с

16. Робототехника и гибкие автоматизированные производства: В 9 кн. Кн.3. Управление робототехническими системами и гибкими автоматизированными производствами: Учеб.пособие для втузов/И.М.Макаров. В.З.Рахманкулов, В.М.Назаретов и др.; Под ред. И.М.Макарова. М.: Высш.шк., 1986. 159 с.

17.  Флейшман Б.С. Основы системологии. М.: Радио и связь, 1982. 362 с.

18. Яни Э. Прогнозирование научно-технического прогресса: Пер. с англ. М.: Прогресс. 1974. 376 с