Оптимальный выбор структуры ГПС в условиях неопределенности развития производства, страница 7

В соответствии с принципами построения ГПС к ТО предъявляются следующие требования:                                                    

- состав ТО обуславливается конструкторско-технологическими особенностями группы изготавливаемых изделий;

-  максимальная концентрация операций на отдельных единицах ТО, что позволяет сократить количество единиц оборудования, улучшить качество обработки и сократить продолжительность производственного цикла;

- полная автоматизация ТО, включая загрузку заготовок и выгрузку готовых деталей;

-  постоянство базирования деталей при переносе их с одного вида оборудования на другой;

-  возможность быстрой автоматической переналадки оборудования на другие режимы или смены инструмента;

-  компоновочная и программная стыковка ТО разных видов е транспортной и измерительной системами;

-  быстрая переналадка технологической оснастки, использование унифицированной групповой тары-спутника;

- автоматическое удаление и утилизация отходов производства.

Очевидно, что указанные требования в большинстве своем противоречивы и отражают лишь общие тенденции развития ТО. В наибольшей степени этим требованиям отвечают элементы ТО с ЧПУ, ввиду высокой степени автоматизации процессов и скорости переналадки. Такие технологические элементы ГПС называют ГПМ.

Поскольку ТП можно представить с помощью маршрутов, т.е. последовательности технологических операций, которые реализуются на определенном ТО, то можно для каждого ТП составить совокупность ГПМ, реализующих данный ТП.         

В общем виде ГПМ могут быть классифицированы по принадлежности к тем или иным подсистемам ГПС. Основные типы ГПМ:

- гибкий производственный технологический модуль, представляющий единицу ТО, управляемую от микроЭВМ и снабженную промышленным роботом (ПР) для загрузки и выгрузки;

- гибкий производственный модуль склада;

- гибкий производственный транспортный модуль, представляющий транспортное средство с программным управлением;

- гибкий производственный контрольно-измерительный модуль.

С помощью таких ГПМ можно комплектовать любые технологические системы. Однако в настоящее время выбор серийно выпускаемых  ГПМ ограничен. Наиболее широкое распространение нашли металлорежущие станки с программным управлением и обрабатывающие центры. Однако номенклатура операций ТП производства аппаратуры насчитывает около 1000 операций. Естественно, что объемы производства ГПМ по всем этим операциям различны, что приводит к необходимости унификации элементов ГПМ, начиная от системы подачи заготовок, выгрузки готовых изделий, систем управления и т. д.

ЗАДАЧИ  МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ  В

ТЕХНОЛОГИИ ПРОИЗВОДСТВА ЭА

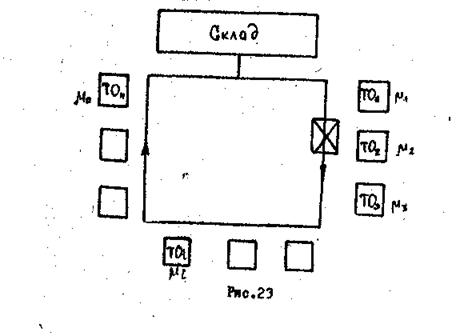
5.1. Задача оптимальной загрузки транспортного устройства

На производстве имеется транспортная система, обслуживающая  единиц ТО (рис. 23). Транспортная система характеризуется грузоподъемностью  Р и полезным объемом V . На каждую  -ю единицу ТО транспортная система должна поставить детали -го типа, характеризующиеся массой , и объемом . Полезность перевозки детали -го
типа по заданному маршруту пропорциональна производительности     ТО, для которого она предназначена, , т.е. чем больше производительность ТО, тем большее количество деталей необходимо к нему доставить.

Задача состоит в том, чтобы определять количество  деталей -го типа, , которое необходимо загрузить в транспортное устройство, чтобы полезность перевозки деталей была бы максимальной. При этом загрузка всего ТО также будет максимальной. Подобные задачи относятся к задачам математического программирования. В качестве
целевой функции, очевидно, следует выбрать суммарную полезность перевозки деталей

  .

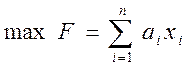Ограничения на независимые переменные устанавливается по грузоподъемности и полезному объему транспортного устройства. Ограничение по грузоподъемности заключается в том, что суммарная масса деталей, перевозимых транспортным устройством, не должна превышать его грузоподъемности

  .

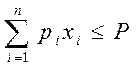Ограничение по полезному объему аналогично

  .

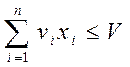В данном случае и целевая функция  и ограничения является линейными, поэтому задача математического программирования относится к задачам линейного программирования.

5.2. Геометрическая интерпретация задачи линейного программирования  

Задача линейного программирования имеет простую геометрическую интерпретацию. В евклидовом   -мерном пространстве система ограничений определяет некоторый выпуклый  многогранник  (рис.24).  Для выяснения геометрической сущности целевой функции приравняем  ее нулю

 .

Полученное уравнение определяет в   -мерном пространстве гиперплоскость, проходящую через начало координат перпендикулярно вектору при     (рис.24а).

Для нахождения максимума необходимо гиперплоскость отодвинуть параллельно самой себе в направлении вектора     как можно дальше от начала координат, но так, чтобы с областью допустимых решений оставалась хотя бы одна общая точка   R   . Аналогично,  минимум будет находиться в точке S . На этом основан графический метод решения задачи с двумя неизвестными

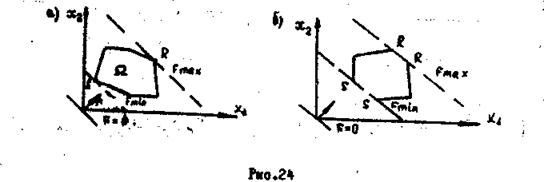
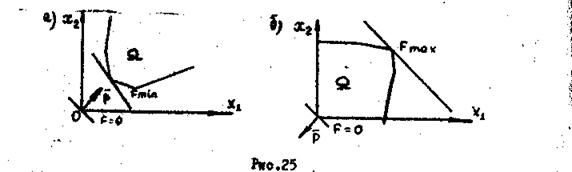
Если гиперплоскость параллельна ребру или грани области , то решений будет бесчисленное множество - все точки ребра или грани (рис.24,б).  Если множество   не ограничено сверху, то гиперплоскость можно передвигать сколь угодно далеко (рис.25,а). Функционал в данном случае не ограничен и задачу на  решить невозможно, хотя на   задача решается. В случае, если не введены ограничения снизу, в том числе и , то подобная ситуация может сложиться при решении задачи на минимум (рис.25,б). При условии значения функционала снизу всегда ограничены нулем.

Понятно, что графически задача решается только на плоскости, размерность которой равна двум. Для более сложных случаев разработан специальный метод нахождения экстремумов – симплекс-метод. В основе его лежит то свойство задачи,что система ограничений определяет в -мерном евклидовом пространстве выпуклый многогранник, в одной из вершин которого достигается экстремум целевой функции.