5.10. Разработка технологического процесса функциональной подгонки аналоговых микросборок на основе АRC-фильтров
Проектирование технологических процессов регулировки интегральных схем и микросборок в научно-технической литературе обычно называют "функциональной подгонкой". Термин "функциональная" определяет тот факт, что регулировка осуществляется по отклонениям выходных контролируемых параметров от номинальных значений и считается законченной, когда эти отклонения попадают в пределы установленных допусков. В связи с тем, что регулировка интегральных схем и микросборок осуществляется с помощью специальных конструкций подгоняемых элементов (плавно-подгоняемые и дискретно-подгоняемые пленочные структуры) и специальным оборудованием (лазеры, электроискровые установки и пр.) изменяющим геометрическую форму или электрофизические свойства материалов подгоняемых элементов, и характеризуется высокой сложностью перерегулировок, свойственным подгоночным операциям, то по аналогии с подгонкой отдельных элементов схемы и регулировка микросборок и интегральных схем стала называться "функциональной подгонкой /25,32,40,50,56 и др./.
Основным недостатком существующих подходов к проектированию процессов функциональной подгонки является стремление получить универсальную группу регулируемых элементов, позволяющую подгонять узлы МЭА во всей области разбросов выходных параметров, что в значительной мере усложняет алгоритмы и не всегда приводит к сходимости процесса регулировки /8,35,40,135 и др./.
Таким образом, предварительная технологическая классификация регулируемых узлов МЭА на группы, соответствующие оптимальным областям поля рассеяния выходных параметров для подгонки заданной группой регулируемых параметров, позволит значительно повысить выход годных на операции функциональной подгонки, хотя при этом возникает необходимость уточнения математических моделей регулируемых узлов, исследования статистических характеристик чувствительностей регулируемых параметров и, следов распределения погрешностей выходных параметров в зависимости от величины удельного поверхностного сопротивления резисторов пленочной пассивной части микросборок.
В данном разделе рассмотрим методику построения технологического процесса функциональной подгонки аналоговых микросборок, представленных линейной моделью.
Постановка задачи реализации процесса функциональной подгонки непосредственно связана с физической реализацией методов нелинейного программирования применительно к оптимизации параметров аналоговых микросборок /1,27,35,50,56,172,175 и др./. В настоящее время существует несколько постановок этой задачи.
Наиболее распространенной является задача минимизации затрат на функциональную подгонку при выполнении требований к точности выходных контролируемых параметров /56,58,59,64 и др./. В тех случаях, когда затраты на функциональную подгонку малы или не беруться в расчет, то задача построения процесса функциональной подгонки сводится к задаче минимизации специально сформированного критерия в виде нормы отклонений выходных контролируемых параметров в евклидовом или чебышевском пространстве /50 и др./. При этом задача проектирования процесса функциональной подгонки сводится к задаче поиска экстремума целевой функции с помощью градиентных методов, базирующихся на основных выводах теории чувствительности и теории операций.
В качестве целевых функций используются:
- эвклидова норма вектора выходных контролируемых параметров
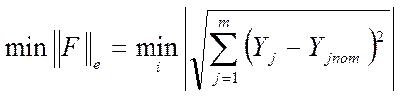 ;
;
норма вектора выходных контролируемых параметров в чебышевском пространстве /50/
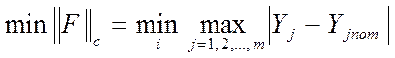 ;
;
где ![]() ;
; ![]() -
номинальное значение
-
номинальное значение ![]() -го выходного параметра,
при
-го выходного параметра,
при ![]() , а следовательно и последовательности
действий при регулировке разбиваются на две части:
, а следовательно и последовательности
действий при регулировке разбиваются на две части:
- определение составляющих градиента, т.е. оптимальный выбор достаточной группы подгоняемых элементов схемы;
- организации движения системы к точке экстремума, т.е. создание методики точного задания действий в процессе функциональной подгонки.
Первичные параметры схемы, всегда можно разделить на группы:
- первичные параметры, которые могут быть регулируемыми - ![]() ;
;
- первичные параметры, которые не могут быть регулируемыми в данной
конструкции и технологических условиях или, регулировка иx нецелесообразна по
экономическим или надежностным ограничениям - ![]() .
.
Выбор подгоняемых элементов, как правило, осуществляется на основе
анализа матрицы чувствительностей регулируемых первичных параметров ![]()
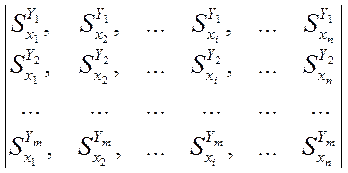
выходных
контролируемых параметров ![]() ,
, ![]() к вариациям первичных параметров
к вариациям первичных параметров ![]() .
.
Среди регулируемых первичных параметров ![]() можно
выделить параметры
можно
выделить параметры ![]() , которые влияют на
изменение лишь одного выходного параметра
, которые влияют на
изменение лишь одного выходного параметра ![]() .
В этом случае, в столбце матрицы чувствительностей, соответствующем данному
параметру все чувствительности кроме
.
В этом случае, в столбце матрицы чувствительностей, соответствующем данному
параметру все чувствительности кроме ![]() будут
равны нулю и подгонка этим первичным параметром
будут
равны нулю и подгонка этим первичным параметром ![]() выходного
контролируемого параметра
выходного
контролируемого параметра ![]() будет независима.
Группа первичных параметров, каждый из которых одновременно влияет на
несколько выходных контролируемых параметров. Степень влияния вариации
первичного параметра и направление изменения выходного контролируемого параметра
при этом определяется величиной и знаком чувствительности.
будет независима.
Группа первичных параметров, каждый из которых одновременно влияет на
несколько выходных контролируемых параметров. Степень влияния вариации
первичного параметра и направление изменения выходного контролируемого параметра
при этом определяется величиной и знаком чувствительности.
Следовательно, в первом приближении относительные чувствительности ![]() ,
,![]() ,…,
,…,![]() ,…,
,…,![]() являются
составляющими вектора градиента в пространстве отклонений выходных
контролируемых параметров
являются
составляющими вектора градиента в пространстве отклонений выходных
контролируемых параметров 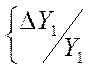 ,
,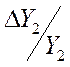 ,…,
,…,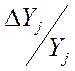 ,…,
,…,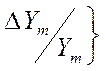 при положительном единичном приращении
первичного параметра
при положительном единичном приращении
первичного параметра 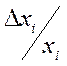 .
.
При этом в точке номинальных значений выходных контролируемых параметров целевая функция будет достигать экстремума, т.е.
![]() .
(5.84)
.
(5.84)
Градиент многомерного вектора ![]() можно записать в
виде матрицы частных производных по регулируемым параметрам
можно записать в
виде матрицы частных производных по регулируемым параметрам ![]() .
.
Поиск экстремума осуществляется градиентными методами, представляющими
собой итеративные процессы. На ![]() -й итерации с
учетом вектора регулируемых параметров
-й итерации с
учетом вектора регулируемых параметров ![]() определяется
градиент
определяется
градиент ![]() , а затем делается шаг вдоль
градиента для нахождения следующего значения вектора
, а затем делается шаг вдоль
градиента для нахождения следующего значения вектора ![]() ,
т.е.
,
т.е.
![]() ,
,
где ![]() - коэффициент определяющий ширину
шага.
- коэффициент определяющий ширину
шага.
Процесс поиска заканчивается при выполнении условия (5.84). Точность
приближения к минимуму зависит от величины коэффициента ![]() . Ошибка в определении значения
. Ошибка в определении значения ![]() приводит к тому, что на (
приводит к тому, что на (![]() )-й итерации экстремум будет пройден,
а вернуться назад невозможно, так как в процессе функциональной подгонки
параметры регулируемых элементов изменяются только в одну сторону. Поэтому в
таких случаях приходится вводить подгонку параметров других пассивных
элементов в направлении, обратном направлению градиента.
)-й итерации экстремум будет пройден,
а вернуться назад невозможно, так как в процессе функциональной подгонки
параметры регулируемых элементов изменяются только в одну сторону. Поэтому в
таких случаях приходится вводить подгонку параметров других пассивных
элементов в направлении, обратном направлению градиента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.