Кроме того, при функциональной подгонке, одновременное изменение параметров регулируемых элементов технически трудно осуществимо. Поэтому, как правило, организуются последовательные процедуры поиска экстремума типа алгоритма Гаусса-Зейделя.
Исследования вариаций чувствительностей гибридно-пленочных микросборок
/21,32,56,64,65,137 и др./ в условиях больших разбросов удельных поверхностных
сопротивлений ![]() показало, что сами чувствительности
являются функциями первичных параметров и, при случайных их отклонениях и
сильных корреляционных связях между параметрами пленочных пассивных элементов
имеют разбросы (поля рассеяния) соизмеримые с разбросами первичных параметров.
Для двумерного случая этот факт можно представить в виде векторной диаграммы
рис. 5. 17. При этом случайную величину
показало, что сами чувствительности
являются функциями первичных параметров и, при случайных их отклонениях и
сильных корреляционных связях между параметрами пленочных пассивных элементов
имеют разбросы (поля рассеяния) соизмеримые с разбросами первичных параметров.
Для двумерного случая этот факт можно представить в виде векторной диаграммы
рис. 5. 17. При этом случайную величину ![]() в
первом приближении можно определить, ее полем рассеяния
в
первом приближении можно определить, ее полем рассеяния ![]() . Тогда вектор направления движения
системы при вариации
. Тогда вектор направления движения
системы при вариации ![]() , при различных сочетаниях
первичных параметров влияющих на выходной контролируемый параметр
, при различных сочетаниях
первичных параметров влияющих на выходной контролируемый параметр ![]() будет находится в пределах
заштрихованной области и, в общем случае определяться многомерной плотностью
распределения вероятностей.
будет находится в пределах
заштрихованной области и, в общем случае определяться многомерной плотностью
распределения вероятностей.
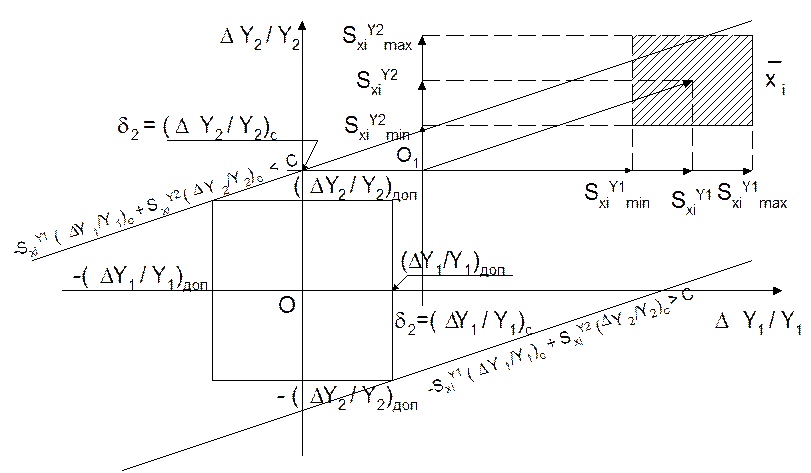 Рис. 5.17. Векторная диаграмма чувствительностей в пространстве
координат
Рис. 5.17. Векторная диаграмма чувствительностей в пространстве
координат
отклонений выходных контролируемых параметров DY1/Y1 и DY2/Y2.
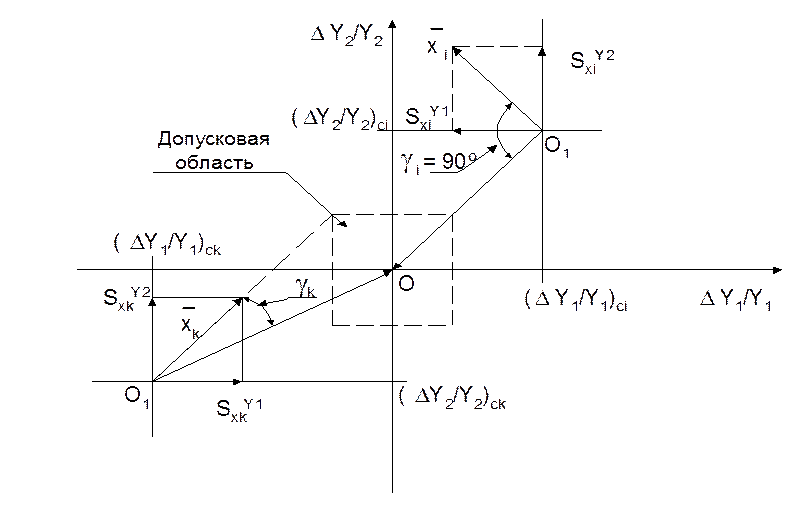
Рис. 5.18. Векторная диаграмма определения регулируемого элемента.
Допуски на выходные контролируемые параметры на данной диаграмме будут
представлять собой прямоугольную область ограниченную предельно допустимыми
значениями 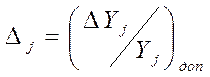 .
.
Случайные отклонения первичных параметров приводят к отклонениям
выходных контролируемых параметров, которые в пространстве их отклонений будут
представлять собой точку О1 с координатами 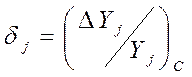 за
пределами допусковой области.
за
пределами допусковой области.
Процесс подгонки в данном случае можно представить как движение системы из точки О1 к точке О, т.е. в пределы заданных допусков. В пространстве отклонений выходных параметров декартово расстояние между этими точками составляет
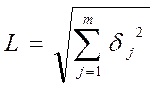 .
.
Вариация первичного параметра ![]() в сторону увеличения
представляется как движение системы в направлении суммарного вектора
в сторону увеличения
представляется как движение системы в направлении суммарного вектора ![]() , модуль которого определяется как
, модуль которого определяется как
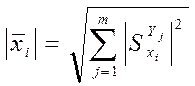 ;
;
при вариации
в сторону уменьшения ![]() движение системы будет
происходить в противоположном направлении.
движение системы будет
происходить в противоположном направлении.
Если направление вектора ![]() совпадает с
направлением ОО1, то приращение подгоняемого первичного параметра
совпадает с
направлением ОО1, то приращение подгоняемого первичного параметра ![]() в относительных единицах будет равно
в относительных единицах будет равно
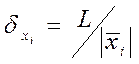 .
.
Количественной характеристикой движения системы с помощью подгоняемого
элемента ![]() можно представить угол
можно представить угол ![]() между направлением О1О к
номинальным значениям выходных контролируемых параметров и направлением вектора
между направлением О1О к
номинальным значениям выходных контролируемых параметров и направлением вектора
![]() (рис.5.18), либо одна из функций
данного угла, например соs
(рис.5.18), либо одна из функций
данного угла, например соs ![]() . Максимальное
значение соs
. Максимальное
значение соs ![]() = 1 означает полное совпадение
направлений подгонки при увеличении регулируемого параметра; при соs
= 1 означает полное совпадение
направлений подгонки при увеличении регулируемого параметра; при соs ![]() = -1 подгоняемый элемент необходимо
изменять в сторону уменьшения. В случае, когда соs
= -1 подгоняемый элемент необходимо
изменять в сторону уменьшения. В случае, когда соs ![]() =
0 - направление движения системы будет перпендикулярным к оптимальному
направлению подгонки.
=
0 - направление движения системы будет перпендикулярным к оптимальному
направлению подгонки.
Функция соs ![]() может быть легко
представлена через скалярное произведение векторов измеренных отклонений
выходных контролируемых параметров
может быть легко
представлена через скалярное произведение векторов измеренных отклонений
выходных контролируемых параметров 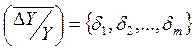 и вектором
и вектором ![]()
![]() ,
,![]() ,…,
,…,![]() ,…,
,…,![]()
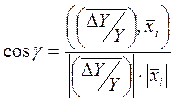 ,
,
Здесь 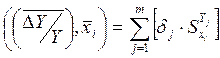 - скалярное произведение
векторов
- скалярное произведение
векторов 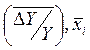 ;
; 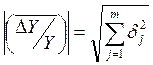 ,
,
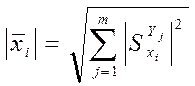 - модули векторов, соответственно
- модули векторов, соответственно 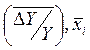 .
.
Тогда при подгонке одним регулируемым элементом для всего множества ![]() рассчитывают множество
рассчитывают множество ![]() ,
, ![]() ,…,
,…,
![]() для соответствующих измеренных
отклонений
для соответствующих измеренных
отклонений 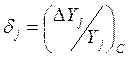 . Для подгонки необходимо
использовать элемент с
. Для подгонки необходимо
использовать элемент с ![]() -м параметром для которого
-м параметром для которого
![]()
![]() ,
, ![]() ,…,
,…, ![]() .
.
В том случае, если величина ![]() имеет
отрицательный знак, то подгонка должна осуществляться в сторону уменьшения
параметра.
имеет
отрицательный знак, то подгонка должна осуществляться в сторону уменьшения
параметра.
Для каждого ![]() -го подгоняемого элемента
можно задать область
-го подгоняемого элемента
можно задать область ![]() , величина которой зависит
от направления вектора
, величина которой зависит
от направления вектора ![]() и размеров допусковой
области D, в пределах которой все узлы с отклонениями
и размеров допусковой
области D, в пределах которой все узлы с отклонениями 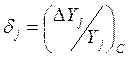 ,
,
![]() попадающими в эту область, могут
быть подогнаны в пределы допуска. Судя по рис. 5. 17 границы области
попадающими в эту область, могут
быть подогнаны в пределы допуска. Судя по рис. 5. 17 границы области ![]() могут быть заданы
ограничениями
могут быть заданы
ограничениями
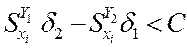 ,
,
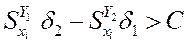 ,
,
где 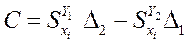 .
.
В общем случае можно задать систему линейных неравенств
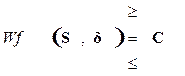
определяющих
положение области ![]() в пространстве отклонений
выходных контролируемых параметров.
в пространстве отклонений
выходных контролируемых параметров.
Подгонка одним регулируемым элементом дает возможность резко сократить
затраты. Если подгонка данным элементом невозможна, то есть движение системы в
направлении вектора ![]() не позволяет попасть в
допусковую область, то необходимо выбрать второй регулируемый элемент
не позволяет попасть в
допусковую область, то необходимо выбрать второй регулируемый элемент ![]() с направлением ортогональным
направлению
с направлением ортогональным
направлению ![]() . В этом случае возможна подгонка
узлов в плоскости, образованной векторами
. В этом случае возможна подгонка
узлов в плоскости, образованной векторами ![]() и
и
![]() , а при подгонке двух контролируемых
выходных параметров (рис. 5.18) узлы с любыми отклонениями выходных параметров
могут быть подогнаны в допусковую область. При этом следует учитывать
технологические ограничения, связанные с направлениями подгонки регулируемых
элементов и, положением и размерами полей рассеяния выходных контролируемых
параметров.
, а при подгонке двух контролируемых
выходных параметров (рис. 5.18) узлы с любыми отклонениями выходных параметров
могут быть подогнаны в допусковую область. При этом следует учитывать
технологические ограничения, связанные с направлениями подгонки регулируемых
элементов и, положением и размерами полей рассеяния выходных контролируемых
параметров.
При увеличении размерности пространства выходных контролируемых
параметров ![]() , очевидно, подгонка из любой точки
отклонений выходных контролируемых параметров может быть осуществлена c
помощью
, очевидно, подгонка из любой точки
отклонений выходных контролируемых параметров может быть осуществлена c
помощью ![]() регулируемых параметров. Этот случай
возникает тогда, когда отсутствует информация о расположении полей рассеяния
регулируемых параметров. Этот случай
возникает тогда, когда отсутствует информация о расположении полей рассеяния 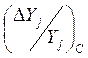 .
.
Для двумерного случая (рис.5.18 ) векторы регулируемых элементов ![]() и
и ![]() должны
быть ортогональны, т.е. скалярное произведение
должны
быть ортогональны, т.е. скалярное произведение
![]() , (5.85)
, (5.85)
а модули этих
векторов - равны ![]() .
.
В противном случае регулировка в направлении перпендикулярном вектору ![]() будет приводить к значительным
приращениям при подгонке регулируемых параметров, и возможному выходу за пределы
области работоспособности схемы /58,64/.
будет приводить к значительным
приращениям при подгонке регулируемых параметров, и возможному выходу за пределы
области работоспособности схемы /58,64/.
Cреди множества регулируемых параметров ![]() для
реальных схем может не найтись векторов удовлетворяющих требованиям (5.85).
В этом случае необходимо выбирать векторы регулируемых параметров с минимальным
значением скалярного произведения и наиболее близкие по модулю.
для
реальных схем может не найтись векторов удовлетворяющих требованиям (5.85).
В этом случае необходимо выбирать векторы регулируемых параметров с минимальным
значением скалярного произведения и наиболее близкие по модулю.
При подгонке необходимо обеспечить общее движение системы (компенсации
погрешностей 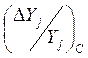 к центру системы координат
О. Для этого необходимо, чтобы результирующий вектор направления движения
к центру системы координат
О. Для этого необходимо, чтобы результирующий вектор направления движения ![]() совпадал или отклонялся на
минимальный угол относительно направления О1О. Для общего случая
положение вектора
совпадал или отклонялся на
минимальный угол относительно направления О1О. Для общего случая
положение вектора ![]() можно представить в
следующем виде
можно представить в
следующем виде
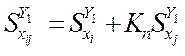
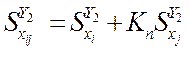 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.