Разработка технологического процесса функциональной подгонки аналоговых микросборок на основе АRC-фильтров, страница 3

где 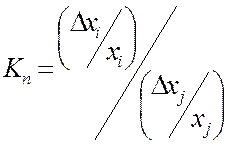  -  отношение относительных приращений при подгонке по регулируемым параметрам  и . То есть если регулиру­емому параметру  задано, при подгонке, единичное приращение, то переменной  должно быть задано приращение , при этом сохранить­ся общее направление движения системы.

Угол между векторами О¹О и  может быть определен через его косинус , а подгонка в направлении к центру координат О должна задавать направление вектора  таким образом, чтобы , т.е. для двумерного случая

  .

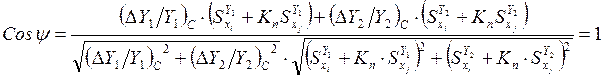Решая это равенство относительно  получим

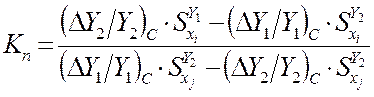   .               (5.86)

Полученное выражение (5.86) позволяет для любых случайных отк­лонений выходных контролируемых параметров 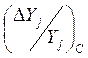 и регулируемых элементов  и  получить соотношение приращений, приводящее к движению системы (в смысле компенсации погрешностей) по направлению к началу координат О, т.е. к точке номинальных значений выходных контролируемых параметров.

Такой подход позволяет разбить пространство отклонений выход­ных контролируемых параметров 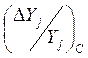  на классы, соответствующие различным значениям , т.е. различным направлениям подгонки, выра­жающимся в различных соотношениях приращений регулируемых парамет­ров при подгонке.

Разбиение на классы может быть представлено в виде таблиц или графиков зависимости  от величин отклонений 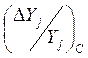 и чувстви­тельностей выходных контролируемых параметров к вариациям регулиру­емых параметров , .

Для полной компенсации отклон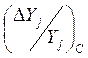ений   выходных контроли­руемых параметров модуль вектора приращений  должен быть равен модулю вектора  , т.е.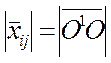

.

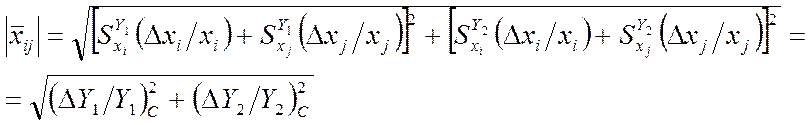Учитывая, что  ,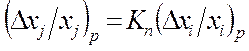

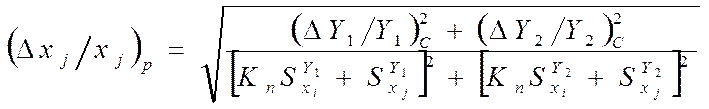    ,       (5.87)

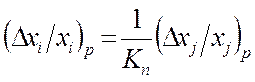   ,                                                                                         (5.88)

где  ,  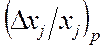 - приращения параметров регулируемых эле­ментов  и  при подгонке, необходимые для полной компенсации отклонений   и  .

Рассмотрим пример разработки методики функциональной подгонки для линейной схемы звена фильтра нижних частот рис.5.19. Передаточ­ная функция этой схемы получена в п.3. Подставляя конкретные параметры элементов схемы получим

  ,

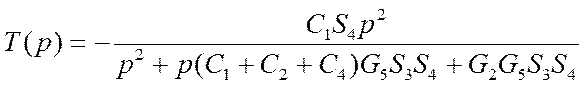где ,  .

Основными выходными контролируемыми параметрами этой схемы яв­ляются:

- затухание полюса

  ;

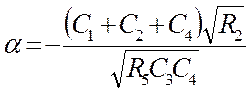- граничная частота

   .

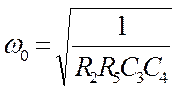Номинальные значения первичных параметров , поля рассеяния первичных параметров  и чувствительности  и  приведены в табл.5.4.  Для выбора пары регулируемых элементов воспользу­емся соотношениями (5.85).  Положения векторов , , ,  и мо­дулей 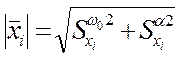   приведены на рис.5.20.

Из рис.5.20 следует, что среди первичных параметров, ортога­нальными являются векторы сооответствующие параметрам R₂ и R₅. При этом, модули этих векторов равны.

В табл.5.5 приведены значения  (5.86), полагая, что прираще­ние  регулируемого элемента R₅ является единичным, для полей рассеяния выходных параметров  и  равных +15% с интерва­лами 5%. Табл. 5.5 может быть представлена в виде графиков рис.5.21.

Для того,  чтобы воспользоваться графиком рис.5.21, необходимо замерить значения   и  контролируемого образца схе­мы. По этим значениям, с помощью рис.5.21 определяется значение . Тогда направление подгонки (компенсации погрешностей выходных конт­ролируемых параметров   и  ) будет определяться век­тором, составляющие которого будут равны  и .

Значения  близкие  и  определяют области в пространстве отклонений выходных контролируемых параметров соот­ветствующие подгонке одним регулируемым элементом: в первом случае параметром R₅, во втором - R₂.

Для примера на рис.5.22 представлены варианты организации про­цесса функциональной подгонки из различных точек пространства вы­ходных контролируемых параметров.

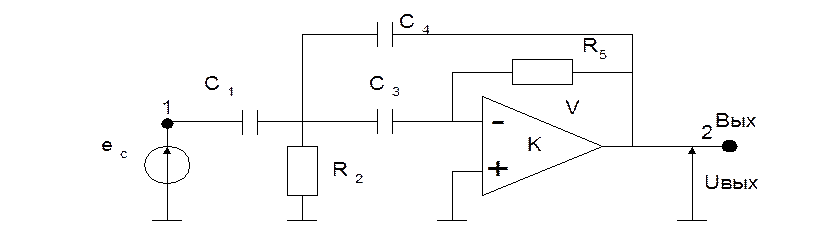
                             Рис. 5.19. Принципиальная схема звена ARC-фильтра верхних частот

                                                                                                                                 Таблица 5.4.

Исходные данные для проектирования процесса функциональной подгонки

ARC-фильтра верхних частот

Параметр	R2	R5	C1	C3	C4
x i nom	3,3 кОм	30кОм	10нФ	10нФ	10нФ
d i	10%	10%	15%	15%	15%
Sxi a	0,5	-0,5	0,33	-0,16	-0,16
Sxi w	-0,5	-0,5	-	-0,5	-0,5

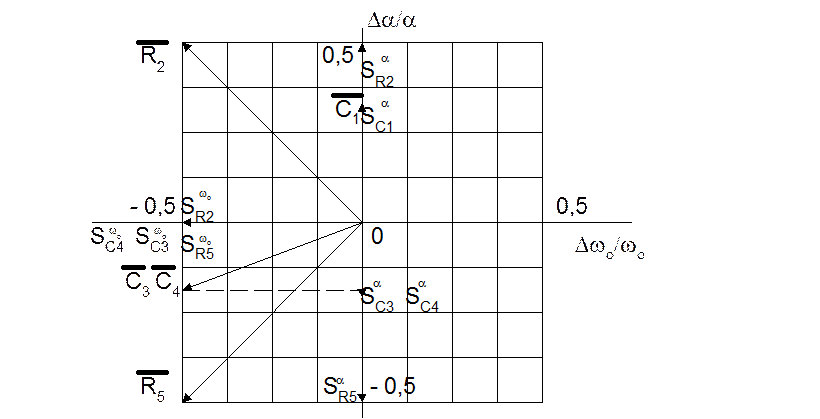
              Рис. 5.20. Векторы параметров элементов схемы звена ARC-фильтра верхних

              частот в пространстве отклонений выходных контролируемых параметров

Наличие ограничений, присущих гибридно-пленочной технологии производства электронной аппаратуры, приводит к некоторому измене­нию представленной выше методики функциональной подгонки. Так, нап­ример, сложность установки регулируемых емкостей в гибридных интег­ральных микросборках приводит к тому, что для рассматриваемой схемы ARC-фильтра верхних частот емкости не могут быть регулируемыми эле­ментами. Подгонка резисторов в сторону увеличения сопротивления также накладывает определенные ограничения.

                                                                                                                             Таблица 5.5.

         Таблица значений Кп = (DR2/R2)/(DR5/R5), при (DR5/R5 ) = 1, в пространстве отклонений

          выходных контролируемых параметров Da/a и Dwo/wo

	Dwo/wo
Da/a	-15%	-10%	-5%	0	5%	10%	15%
-15%		-5	-2,5	-1	-0,4	-0,2	0
-10%	5		-3	-1	-0,33	0	0,2
-5%	2	3		-1	0	0,33	0,5
0	1	1	1	-	1	1	1
5%	0,5	0,33	0	-1		3	2
10%	0,2	0	-0,33	-1	-3		5
15%	0	-0,2	-0,4	-1	-2,5	-5

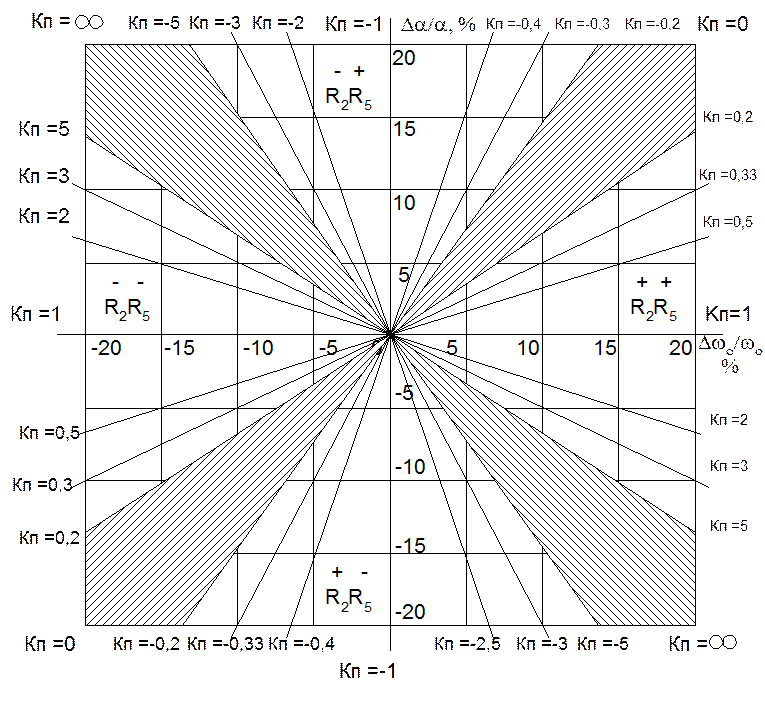
                Рис. 5.21. График распределения Кп (направлений подгонки) в пространстве  

                            отклонений выходных контролируемых параметров Da/a и Dwo/wo

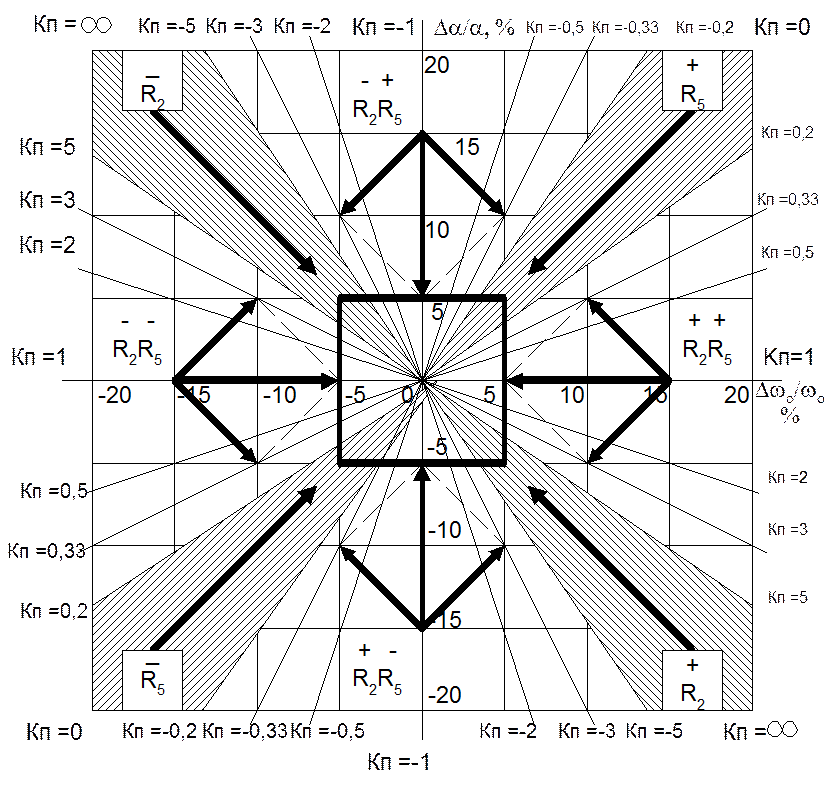
                 Рис.5.22. Варианты стратегий функциональной подгонки из различных областей

                             пространства отклонений выходных контролируемых параметров ARC-

                             фильтра верхних частот