Разработка технологического процесса функциональной подгонки аналоговых микросборок на основе АRC-фильтров, страница 4

Следовательно секторы (рис.5.21) пространства отклонений вы­ходных контролируемых параметров, для которых  и левый сектор с подгонкой в сторону уменьшения регулируемых параметров R₂,  R₅, не могут быть использованы для регулировки.

Таким образом, для регулировки выходных контролируемых пара­метров  и  с помощью подгонки сопротивлений R₂, R₅ в сторону уве­личения, поля рассеяния отклонений выходных параметров должны нахо­диться в пределах правого сектора +45^o.

5.11. Статистические алгоритмы функциональной подгонки аналоговых микросборок на основе АRC-фильтров

Проблемы функциональной подгонки значительно усложняются при увеличении требований к точности выходных контролируемых параметров и значительных разбросах погрешностей пленочных элементов пассивной части микросборок, а также достаточно больших разбросах параметров навесных компонентов.

Эта ситуация особенно осложняется случайным характером чувс­твительностей выходных контролируемых параметров в зависимости от вариаций первичных параметров элементов схемы.

В условиях такой неопределенности попадание в допусковую об­ласть связано с многошаговым алгоритмом реализации функциональной подгонки при действии случайных помех.

В данном разделе рассмотрим стохастическую модель функциональ­ной подгонки, которая является локально-линейной причем ее градиен­тное направление образуется марковским процессом с заданными корре­ляционными свойствами. При реализации функциональной подгонки в этом случае решаются следующие задачи:

- выбор адекватной функции качества проведения функциональной подгонки;

- выбор необходимого и достаточного количества регулируемых параметров, которым можно задавать случайные значения приращений;

- выбор оптимального расстояния близости текущего состояния системы к его номинальному значению;

- выбор метода накопления при многопараметрической оптимизации методом случайного поиска;

- выбор критериев прекращения случайного поиска.

Функции качества проведения функциональной подгонки позволяют определить свойства поверхности движения системы и рассмотрены в /40,58,59 и др./. Использование квадратической зависимости /40/ позволяет адекватно организовать процесс подгонки с учетом нелиней­ностей поверхности отклика. С другой стороны в области, находящийся в непосредственной близости к точке номинальных значений выходных контролируемых параметров   можно считать, что поверх­ность отклика является линейной и , в этом случае более простой и эффективной является целевая функция, в виде модуля отклонений вы­ходных контролируемых параметров.

В зависимости от условий реализации функциональной подгонки полей рассеяния параметров элементов схемы, величины коэффициента корреляции параметров пленочной пассивной части, величины и знака чувствительностей выходных контролируемых параметров количество ре­гулируемых параметров может изменяться от 1 до n, где n - количест­во выходных контролируемых параметров. Однако в ряде случаев могут использоваться дополнительные регулируемые параметры для осущест­вления прецизионных операций подгонки или корректировки статических режимов работы активных компонентов и условий устойчивости /190/.

В качестве расстояний близости текущего состояния системы к номинальному значению обычно используют евклидово или чебышевское пространство. Так при рассмотрении локальной сходимости поиска вда­ли от экстремума удобно пользоваться линейной моделью:

  ,                           (5.89)

где  - показатель качества модели;   - вектор регулируемых параметров;   - градиент качества; cкобками обоз­начено скалярное произведение.

При изучении поведения процедуры поиска в районе цели  можно воспользоваться центральной моделью:

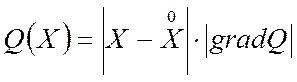    .                                              (5.90)

В настоящее время разработаны ряд эффективных алгоритмов поис­ка экстремума функций качества. В основе этих алгоритмов лежат реа­лизации методов стохастического градиента или случайного отбора на­иболее эффективных направлений поиска.

Пусть в пространстве регулируемых параметров делается шаг в случайном направлении с постоянным модулем и равномерным распреде­лением вероятностей по всем направлениям. Зададимся некоторой вели­чиной , характеризующей приращение функции качества. При этом в процессе поиска возможны три результата соотношений функций качест­ва в новом положении

,                                  (5.91)

 ,                       (5.92)

  .                                     (5.93)

Случайный опыт будет называться результативным, если справед­ливо условие (5.91), т.е. движение системы происходим в направлении к оптимуму с резким уменьшением функции качества (отклонений выход­ных контролируемых параметров. Удачным будем называть опыт, при ко­тором выполняется условие (5.92), и наконец неудачным, при котором выполняется условие (5.93), т.е. движение системы происходит в нап­равлении обратном по отношению к направлению к оптимуму.

Если опыт оказывается результативным, то продолжается движение в том же направлении. Если опыт оказывается удачным, то из нового состояния  производится шаг в случайном направлении. При по­лучении неудачного опыта производится реверс (изменение направления на обратное).

Следует отметить, что для время поиска существенно зависит от величины порога k. Эксперименты показали /2/, что для линейного по­ля, в близи точки номинальных значений выходных контролируемых па­раметров, наибольший эффект получается при выборе k близким к мак­симальному приращению целевой функции.

Для нелинейных поверхностей существует алгоритм адаптации ве­личины k в ходе поиска. Сущность адаптации заключается в следующем. Если в результате проведения случайных опытов N раз подряд опыт оказывается удачным, то k уменьшается в 2 раза: k_i+1 = 0,5^.k_i. Если же N раз подряд опыты оказываются результативными, то k увеличива­ется в два раза, т.е. k_i+1 = 2^.k_i.

Критериями сравнения существующих алгоритмов являются потери на поиск. Обозначим приращение целевой функции , полученное в результате одного шага, через . Как известно в линейном поле ве­личина  пропорциональна косинусу угла  между направлением, об­ратным градиентному, и направлением случайного шага :

 ,                                                 (5.94)

где а - величина рабочего шага в методе градиента.