Разработка технологического процесса функциональной подгонки аналоговых микросборок на основе АRC-фильтров, страница 5

Эффективность методов поиска определяется величиной потерь на поиск, под которыми будем понимать число определений функции ка­чества, необходимое для того, чтобы система в среднем сместилась к цели на величину рабочего шага. Предположим, что перед каждым ра­бочим шагом известно градиентное направление. Тогда для достижения цели потребуется некоторое число шагов М_гр, т.е. М_гр раз определя­ется направление градиента и выполняется рабочий шаг. В действи­тельности для исследуемого алгоритма потребуется количество шагов, отличное от М_гр , т.е. потребуется иное количество измерений целе­вой функции. Обозначим это количество измерений через М. Тогда потери на поиск определяются следующим образом

     ,                                                      (5.95)

где .

Величина 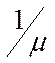 показывает, на какую долю градиентного шага в среднем сместиться система в сторону экстремума при одном поисковом шаге, так как система смещается к цели лишь в результате благопри­ятных шагов, то обозначив число благоприятных шагов через m , будет удобно вместо 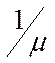 пользоваться понятием среднего смещения не за один поисковый шаг вообще, а за один благоприятный шаг. Тогда сме­щение за один благоприятный шаг

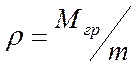    ,                                                           (5.96)

где  .

Если величина градиентного шага , то r будет величиной среднего благоприятного шага при случайном выборе направления дви­жения, т.е. при случайном изменении угла  в интервале . При ;

 .                                                   (5.97)

Математическое ожидание  определяется из выражения

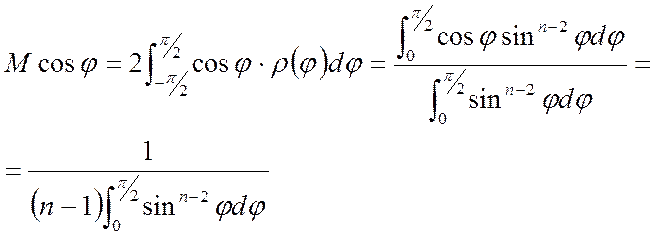,     (5.98)

где 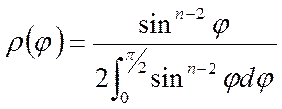    - плотность распределения угла в n-мерном пространстве при равновероятном выборе направлений слу­чайных шагов. Выражение для  впервые было получено Л.А.Растри­гиным /2,118/. Очевидно, что для метода градиента .

Следует отметить, что соотношение (5.98) является применимым для тех алгоритмов случайного поиска, для которых интервал благоп­риятных направлений  не разбит на дискретные части (удачные, результативные и т.д.).

Из выражений (5.95) и (5.96) следует , что

  ,

т.е. для определения потерь на поиск помимо  необходимо вы­числить соотношение  для каждого алгоритма. Это соотношение по­казывает сколько измерений функции качества необходимо произвести, чтобы в среднем получить один благоприятный шаг движения системы.

В связи с тем, что основной особенностью методов случайного поиска является некоторая неопределенность результата оптимизации, связанная со случайным характером самого поиска, естественно, необ­ходимо ввести процедуру накопления, позволяющую улучшить дисперсные свойства случайного поиска.

Рассмотрим два наиболее распространенных вида накопления ин­формации при случайном поиске:

- поиск по наилучшей пробе;

- метод статистического градиента /118/.

Сущность поиска по наилучшей пробе заключается в следующем. Пусть для сбора информации из исходного состояния Х_о делается  случайных пробных шагов. длиной g:

  ,                                            (5.99)

и определяется m значений функции качества:

 ,                                           (5.100)

В соответствие с алгоритмом по наилучшей пробе рабочий шаг де­лается в направлении наибольшего уменьшения функции качества

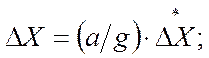                                                                (5.101)

где а - величина рабочего шага, а 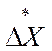 соответствует наилучшей пробе из имеющихся

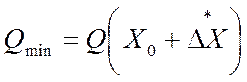   .                                                     (5.102)

Потери на поиск для этого алгоритма выражаются соотношением

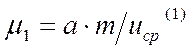,                                                            (5.103)

где 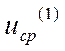 - среднее смещение вдоль градиента на рабочем шаге.

            При  система будет двигаться вдоль градиента функции ка­чества

 ,

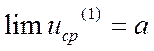а дисперсия проекции рабочего смещения на градиентное направление

  .

На рис.5.23 показано поведение потерь на поиск для этого алго­ритма, а на рис.5.24 поведение дисперсии рабочего смещения для раз­личных значений размерности пространства регулируемых параметров n и числа пробных шагов m. В настоящее время разработано несколько различных модификаций этого алгоритма, отличающихся потерями на по­иск и дисперсией рабочего смещения движения системы от направления градиента.

Второй наиболее распространенный алгоритм случайного поиска - алгоритм статистического градиента, реализует другой способ накоп­ления, где используется значительно большая часть полученной инфор­мации. На базе m+1 проб образуется векторная сумма

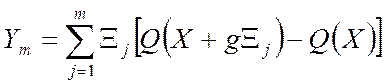  .                                      (5.104)

Относительно этой суммы в случае линейного поля можно выска­зать два очевидных положения, которые являются частным случаем теорем, рассмотренных в работе /118/:

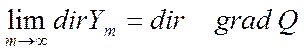 ,                                             (5.105)

где  - направление Z, т.е. с ростом числа проб направ­ление векторной суммы (5.104) стремится к градиентному:

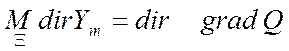  ,                                                (5.106)

т.е. математическое ожидание направления этой суммы по всем возмож­ным реализациям случайных проб  совпадает с градиентным  направле­нием, независимо от числа проб m.

Эти два положения позволяют утверждать, что оценка градиентно­го направления в виде вектора (5.104) будет несмещенной и в пределе при  совпадает с градиентным направлением. Запишем формулу (5.104) в виде рекуррентного соотношения

   ,                                            (5.107)

где  - параметр забывания предыстории,  при этом случай (5.104) соответствует  ; ;  - угол между вектором случайного шага  и направлением градиента функции качества; ;  - величина пробного шага.

Потери на поиск для этого алгоритма выражаются формулой

⁾,                                                          (5.108)

где  - среднее смещение вдоль градиента на рабочем шаге.  На рис. 5.25 представлено поведение среднего рабочего смещения к цели, величины, обратной потерям (5.108) данного алгоритма, для различных значений n  как функции числа проб m при k = 1.  На рис.5.26 показано изменение дисперсии рабочего смещения при движении системы  к  цели как функции числа проб.

Как и следовало ожидать, потери на поиск увеличиваются, а дис­персия уменьшается с увеличением числа проб.

Для сравнения представленных алгоритмов случайного поиска расс­мотрим их характеристики в виде среднего смещения к цели на один шаг  поиска    в            зависимости от дисперсии рабочего смещения  при различных размерностях варьируемых параметров n, представленных на рис.5.27.

Из этого рисунка видно, что кластер соответствующий алгоритму статистического градиента (представлен сплошной линией) имеет преимущество перед алгоритмом поиска по наилучшей пробе как по диспер­сии рабочего смещения так и по среднему смещению на один шаг поис­ка.

Однако с точки зрения сложности реализации алгоритм поиска по наилучшей пробе является значительно проще и предпочтительней при реализации в виде спецвычислителей на основе микропроцессорных комплектов.