Проектирование уравновешивающих механизмов: Методическое пособие, страница 9

·  жесткость пружины , Н/м               

·  начальное усилие поджатия  

5.  Графы таблица 2.1 результатов дополняются расчетом для каждого значения угла возвышения φi текущие значения

·  усилие пружины  (см. 3.1) ,( Н);

·  момент пружинного уравновешивающего механизма

, (Н  м) ;

·  момента неуравновешенности  .

3.2 ПРИМЕР РАСЧЕТА ПО СХЕМЕ «ДВУХ ТОЧЕК»

Форма и результаты расчета в Excel проектируемого пружинного уравновешивающего механизма по данным рассматриваемого примера представлены на рис. 3.2.

По результатам расчетов для визуального сравнения  строятся графики: усилий желаемого и пружины уравновешивающего механизма (рис.3.3), моментов уравновешивающего и качающейся части (рис.3.4). Для построения графиков в Excel используется команда «Вставка – Диаграммы – Точечная» с выбором соответствующих параметров.

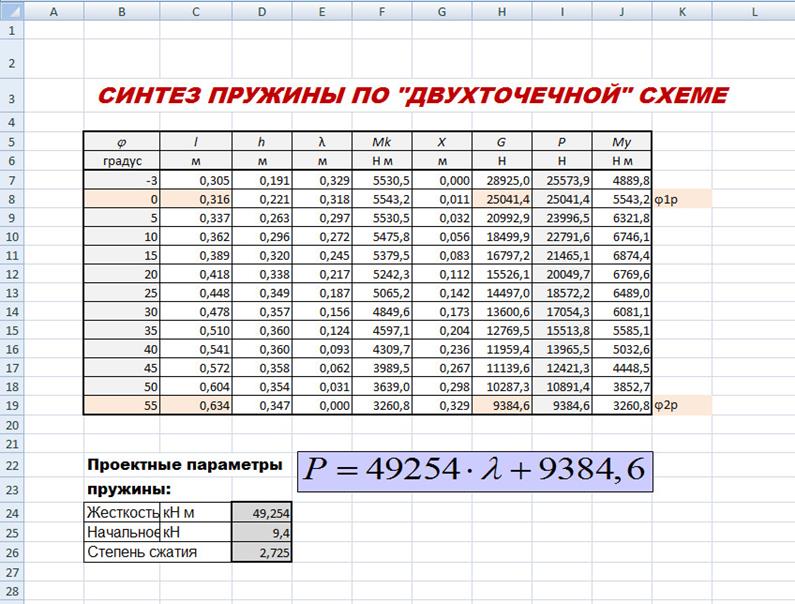
Рисунок  3.2 Лист синтеза пружинного аккумулятора в Excel к рассматриваемому примеру

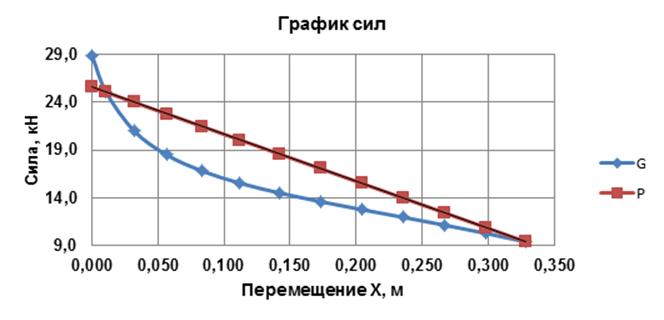
Рисунок  3.3 Графики желаемого усилия и силы пружинного аккумулятора по схеме «двух точек»

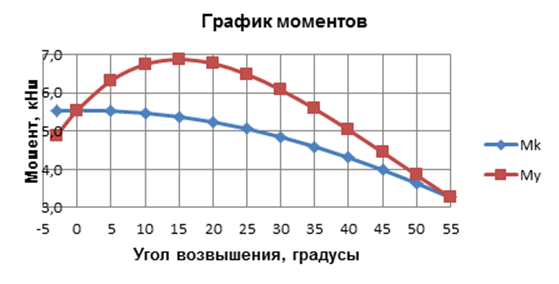
Рисунок  3.4 Графики момента качающейся части (Мк)  и проекта пружинного механизма (Му) по схеме «двух точек»

3.3 СИНТЕЗ ВАРИАНТА ПО СХЕМЕ «ВЗВЕШЕННЫХ НЕВЯЗОК»

Определение оптимальных значений параметров пружинного аккумулятора может быть выполнено путем линеаризации желаемого усилия G методом наименьших квадратов (МНК) – разновидности методов взвешенных невязок.

Так как зависимость усилия пружины (P) от стрелы прогиба (λ) представляется уравнением, близким к линейному (3.1), наилучшее приближение этой зависимости к желаемому усилию G выполняется минимизацией квадрата ошибки e_i=(P_i-G_i):

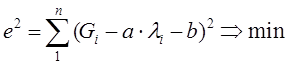, где a= C_pr; b=P_m.

Для минимизации этой функции коэффициенты a и b  линейной зависимости должны удовлетворять условиям:

.

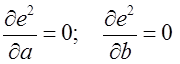Коэффициенты a и b можно вычислить по формулам МНК, используя данные столбцов λi и Gi (табл. 2.1).

В  Excel  эту задачу можно решить без программирования с помощью:

v встроенной функции = ЛИНЕЙН(известные_y, [известные_x], [константа], [статистика]), которая с применением МНК рассчитывает параметры прямой линии, наилучшим образом аппроксимирующей имеющиеся данные;

v процедуры РЕГРЕССИЯ из пакета «Анализ данных»;

v по графику G=G(λ) путем вставки Линия тренда – Линейная.

Наиболее экономично параметры пружины (жесткость и  начальное усилие поджатия пружины) УМ определяются последним способом по графику желаемого усилия G=G(λ). При этом рекомендуется следующий алгоритм:

1.  путем вызова ВСТАВКА – ДИАГРАММА – ТОЧЕЧНАЯ по данные столбцов λi и Gi (табл. 2.1) строится график желаемого усилия G=G(λ);

2.  выделив график полученной функции, вызвать процедуру Добавить линию тренда;

3.  в окне «Формат линии тренда» (рис. 3.5) установить параметр «Линейная» и флажки «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)».

Уравнение на диаграмме представляет собой оптимизированное уравнение пружины. Качество аппроксимации определяется по коэффициенту детерминации (R^2). В зависимости от степени корреляции линии тренда с аппроксимируемыми данными значения R^2 изменяются от 0 (при отсутствии связи) до 1 (при полном совпадении результатов).

3.3  ПРИМЕР РАСЧЕТА ПО СХЕМЕ «ВЗВЕШЕННЫХ НЕВЯЗОК»

Вид графика подбора пружины для данных рассматриваемого примера представлен на рис. 3.6. Результаты расчета примера с параметрами подобранной пружины представлены на фрагменте листа Excel (рис. 3.7).

Поскольку применение данного метода в практике параметрического синтеза пружинных уравновешивающих механизмов ранее не известно, представляет интерес его сравнение с результатами, полученными по «двум точкам» (рис.3.8, 3.9).

Сравнительный анализ двух схем синтеза пружины уравновешивающего механизма показывает, что степень соответствия желаемого усилия и силы пружины, определенной по МНК, значительно выше, чем по схеме «двух точек». Качественно это отражено на графиках (рис.3.8, 3.9), количественно - коэффициентом детерминации (соответственно R^2= 0,842 против R^2= 0,704).