Проектирование уравновешивающих механизмов: Методическое пособие, страница 5

Рисунок 1.8 Устройство пружинного уравновешивающего механизма тянущего типа (100-мм зенитная пушка КС-19)

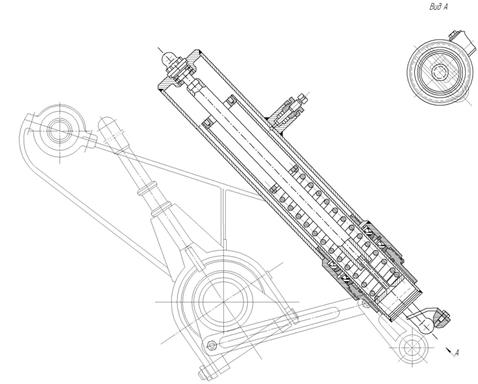
Рисунок 1.9 Устройство пнвмопружинного уравновешивающего механизма толкающего типа (122-мм гаубица Д30)

Рисунок 1.10  3-Д модель цилиндра пнвмопружинного уравновешивающего механизма толкающего типа (122-мм гаубица Д30)

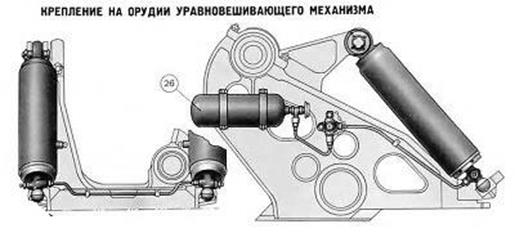
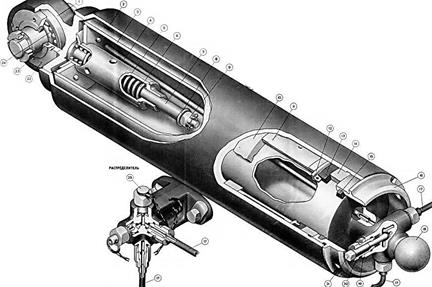
Рисунок 1.11 Схема крепления на орудии и устройство пнвматического уравновешивающего механизма толкающего типа (122-мм пушка М-46 и 152-мм гаубица М-47, самоходная гаубица 2С3М)

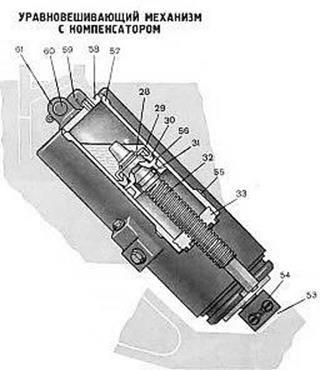
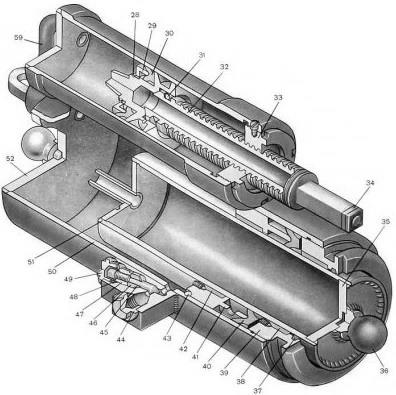
Рисунок 1.12 Схема крепления на орудии и устройство пнвмоцилиндра с компенсатором уравновешивающего механизма толкающего типа (85-мм дивизионная пушка Д-44)

1.4  СХЕМЫ ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КОНСТРУКЦИИ

Синтез представляет собой обратную некорректную задачу, которая выполняется с целью определения численных значений  переменных проектирования  для принятой структурной схемы уравновешивания. 

Задача синтеза проектных параметров может решаться по трем параметрическим схемам:

1.  Теоретически полное уравновешивание;

2.  Неполное уравновешивание по «двум точкам»;

3.  Неполное уравновешивание по «трем точкам»;

4.  Неполное уравновешивание по схеме «оптимизации».

Схема “теоретически полного уравновешивания”

Расчет теоретически полного уравновешивания качающейся части в пределах всего сектора вертикальной наводки возможен для случаев грузового уравновешивания и применения пружинного механизма тянущего типа (рис. 1.3).

В пределах сектора вертикальной наводки  условие теоретически полного уравновешивания пружинным механизмом тянущего типа имеет вид (1.2):

, , где момент силы пружинного уравновешивающего механизма

,

С_pr – коэффициент жесткости пружины; x – ход пружины;

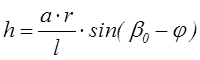 - плечо механизма относительно оси цапф; h=OD.

.

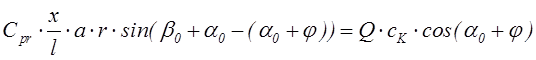Полное уравновешивание может быть достигнуто, при выполнении условий:

v ход пружины при всех допустимых значениях угла ("₀+j) должен быть равным расстоянию между шарнирами А и В, т.е. x=l;

v угол β₀+"₀=B/2, что следует из условия .

Тогда, жесткость пружины вычисляется по формуле

.

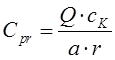Уравновешивание по схеме “двух точек”

При расчете неполного уравновешивания обычно ограничиваются получением теоретически полного уравновешивания качающейся части при каких-либо двух значениях угла возвышения φ (рисунок 1.13) в пределах сектора вертикального обстрела т.е.:

 

или по условию для желаемого усилия

.                           (1.6)                      

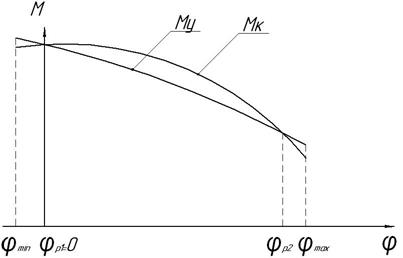
Рисунок 1.13  Уравновешивание в “двух точках”

Сила  должна монотонно убывать с увеличением угла возвышения. Если это условие выполняется, то в качестве расчетных углов принимают: , .

Если не выполняется, то в качестве расчетных углов выбирают: , а второй расчетный угол принимается ближайшим , для которого выполняется условие .

Данная схема не всегда дает хороший вариант параметров уравновешивания. Может быть рекомендована для получения исходного варианта уравновешивания, который затем подвергается оптимизации.

Уравновешивание по схеме “трех точек”

Для уменьшения момента неуравновешенности ΔМ иногда прибегают к уравновешиванию качающейся части в трех точках, т.е ставят задачей обеспечить равенство моментов Мк и Му при трех значениях угла возвышения в пределах сектора вертикального сектора обстрела: .       

Эта схема в настоящее время практически не применяется, т.к. существует более удобная для программной реализации оптимизационная схема.

Уравновешивание по схеме “оптимизации”

Проектный синтез конструкции в общем виде является результатом вариантного перебора параметров уравновешивания и отсеивания из множества возможных конструктивных решений объекта проектирования. В этом случае параметрический синтез представляет собой оптимизационную задачу с ограничениями на множество допустимых решений. Для идентификации варианта выбираются независимые переменные проектирования, однозначно определяющие объект проектирования.