Проектирование уравновешивающих механизмов: Методическое пособие, страница 8

Таблица 2.1 - Предварительный расчет параметров уравновешивания

φi	αi=α0+ φi	βi=β0+ φi	li	λi	hi	Mki	Gi
градус	радиан	радиан	м	м	м	Н •м	Н
Формула			(2.1)	(2.3)	(2.2)	(1.1)	(2.4)
φmin	α1	β1	l1	λ1	h1	Mk1	G1
. φi . .	. αi . .	. βi . .	. li . .	. λi . .	. hi . .	. Mki . .	. Gi . .
φmax	αm	βm	lm	λm=0	hm	Mkm	Gm

Последовательно по правилам Excel в расчетных ячейках программируются представленные ниже формулы и выполняются вычисления параметров по столбцам таблицы.

(Следует иметь ввиду, что тригонометрические функции в Excel вычисляются для аргументов, заданных в радианной мере).

При вычислениях (табл. 2.1) используются следующие выражения:

·  момент   веса   качающейся части (1.1)

  [Н •м], где - постоянная составляющая момента;       

·  расстояние между неподвижным и подвижным шарнирами УМ, т. е. текущее значение АВ                                       

 [м],                                   (2.1)

·  плечо  действия   силы   УМ  относительно оси цапф                                                  

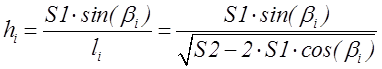    [м],       (2.2)

·  ход  подвижного шарнира А относительно положения при φ_max

  [м],                                               (2.3)

где значение  выбирается из рассчитанных по формуле (2.1)  значений l_i;

·  желаемое усилие аккумулятора уравновешивающего механизма в зоне подвижного шарнира А

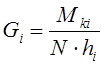, Н.                                                                   (2.4)

2.3 ПРИМЕР РАСЧЕТА ИСХОДНЫХ ПАРАМЕТРОВ

Форма и результаты расчета исходных геометрических и силовых параметров проектируемого уравновешивающего механизма по данным рассматриваемого примера представлены на рис. 2.1.

Графики зависимостей исходных силовых параметров в зависимости от углов возвышения и перемещения подвижного шарнира относительно неподвижного представлены на рис. 2.2 – 2.4. Графики построены по результатам расчетов с помощью встроенных графических средств Excel: «Вставка – Диаграмма – Точечная».

Очевидно (рис. 2.3, 2.4.), что зависимости желаемого усилия от угла возвышения и линейного перемещения подвижного шарнира имеют одинаковый, но взаимообратный, характер.

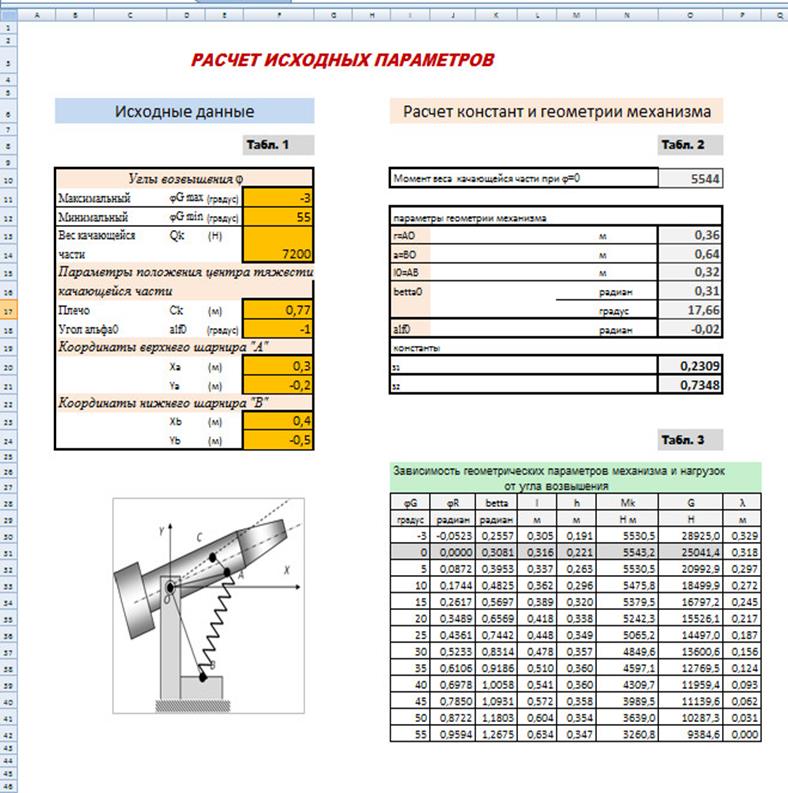
Рисунок 2.1 Лист расчета основных геометрических и силовых параметров примера в Excel

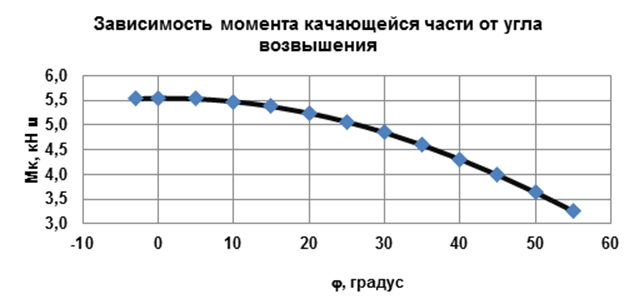
Рисунок 2.2

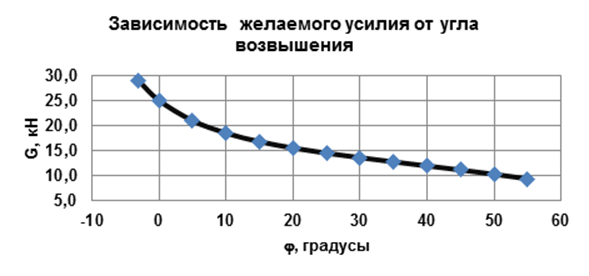
Рисунок 2.3

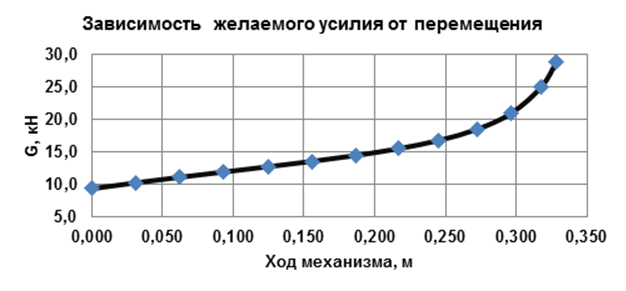
Рисунок 2.4

3  ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ ПРУЖИННОГО АККУМУЛЯТОРА

Зависимость рабочего усилия пружинного аккумулятора, представленного одной пружиной, от хода механизма принято определять линейной функцией (рис. 3.1). Эта зависимость может быть представлена в следующих формах:

;       

где x(j)=l(j)-l(jmin);  λ(j)=l(jmax)-l(j).

Для расчетов наиболее интересна последняя зависимость, которая представима в дискретном виде:

                 (3.1)

где P_m– усилие начального поджатия, соответствующее jmax; C_pr – жесткость пружины.

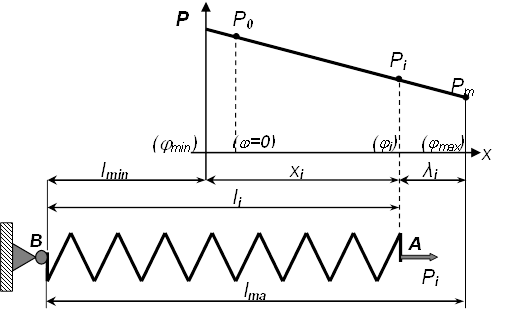Рисунок 3.1 Схема усилия пружинного аккумулятора

3.1 СИНТЕЗ ИСХОДНОГО ВАРИАНТА ПО СХЕМЕ «ДВУХ ТОЧЕК»

Исходной информацией для синтеза аккумулятора является решение задачи, представленной в п. 2.

Параметрический синтез варианта пружины по “2-х точечной” схеме выполняется в следующей последовательности.

1.  Создается рабочий лист книги «Синтез пружины»

2.  Копируются на лист таблица 2.1 результатов с предыдущего листа

Режим копирования: «Специальная вставка – значения и форматы чисел».

3.  Назначаются два расчетных угла j_p1 и  j_p2

Выбор значений углов осуществляется в соответствии с рекомендациями п.1.4

4.  Определяются