Разработка и теоретическое исследование импульсного магнитоэлектрического генератора, страница 7

В нашем случае время t₀, соответствующее  моменту, в который инерционная сила равна усилию магнитного притяжения якоря, по существу, совпадает с временем окончания процесса форсирования (t₀ = 4,34·10 ^{– 3}c).

Разложив sin k (t- t₀) в ряд и пренебрегая членами, выше третьего порядка, получаем:

x (t) = b (t- t₀) ³/6  ,                                                                                (6)

и скорость перемещения якоря

v (t) = b (t- t₀) ² /2  ,                                                                                 (7)

Задаваясь значениями времени t>t₀ и используя формулы (6) и (7), определяем величины скорости перемещения якоря, необходимые для расчета магнитной силы.

Расчеты проводятся до момента, в который перемещение якоря составляет 5 мм. Данные расчета приведены в таблице 1

Таблица 1

t, ms	4,64	4,94	5,1	5,25	5,4	5,55	5,7	5,85	6,0
(t-t0),ms	0,3	0,65	0,80	0,95	1,1	1,25	1,4	1,55	1,7
x , мм	0,034	0,345	0,359	0,45	0,71	1,21	2,033	3,26	4,98
v, м/с	0,085	1,595	1,815	2,67	4,025	5,915	8,345	11,3	14,825

1.5.2 Определение характеристик в зависимости от перегрузки.

Параметры МЭГ:

- начальный магнитный поток Ф₀ = 6000 Мкс = 6·10^-5 Вб;

- число витков обмотки w = 1800;

- омическое сопротивление обмотки R = 200 Ом;

- заданное перемещение якоря x  = 5 мм;

- емкость заряжаемого МЭГ аккумулирующего конденсатора С = 0,44 мкф.

В предыдущем разделе были определены расчетное значение скорости перемещения якоря и время его перемещения на расстояние 5 мм.

Время перемещения якоря на расстояние 4,98 мм равно 1,7 мс. Указанный диапазон времени разбиваем на пять равных расчетных интервалов ∆t = 0,34 мс.

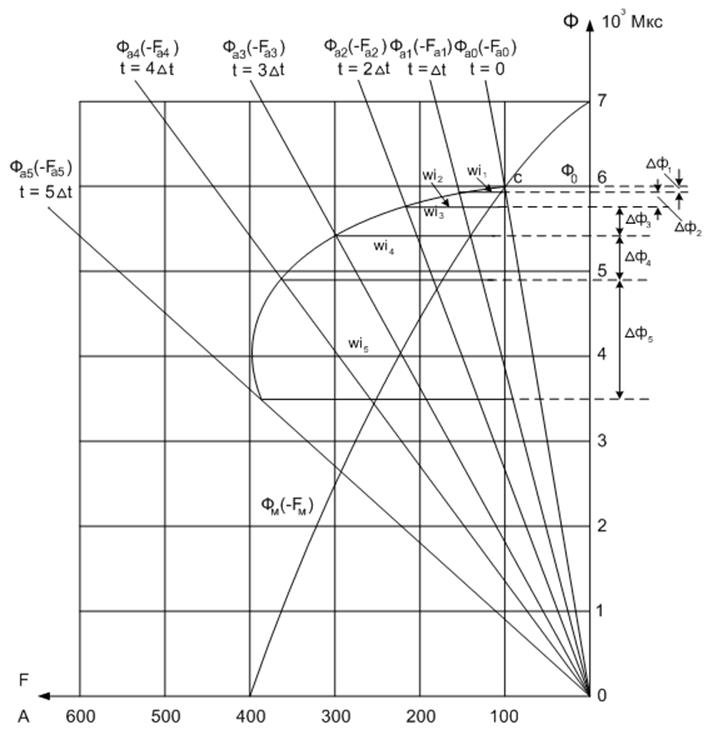
В результате расчета магнитной системы МЭГ для ряда положений якоря, фиксированных через интервалы времени ∆t по методу, изложенному в [2], построена электромагнитная диаграмма генератора (рисунок 2). На диаграмме нанесены кривая размагничивания магнита Ф_м (F_м ) и семейство из шести кривых размагничивания арматуры Ф_а (-F_а ).

Здесь:

Ф_{м –} магнитный поток магнита, сцепленный с обмоткой;

F_{м  -} магнитодвижущая сила магнита;

Ф_{а -} магнитный поток в арматуре

(-F_а ) – взятая с обратным знаком магнитодвижущая сила арматуры.

Уравнение цепи составляется в форме [2]:

Ri + U_c = -w                                                                                    (8)

После преобразований  получается выражение:

wi_k = –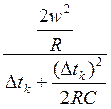·∆Ф_к  – wi_k-1 – 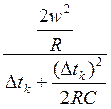··U_c2                                     (9)

Вычислим коэффициенты:

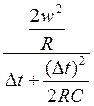 = 0,324·10⁸ ,     = 0,19·10^-6

Уравнение (9) перепишется с численными коэффициентами в виде:

wi_k = – 0,324·∆Ф_к – wi_k-1 – 6,16U_c,k-1                                                                (10)

При этом приращение магнитного потока ∆Ф_к  выражено в максвеллах.

Переходим к расчету отдельных интервалов процесса.

1-й расчетный интервал (к=1)

Так как по начальным условиям i₀ = 0, U_c,0 = 0, то имеем:

wi₁ = - 0,324·∆Ф₁

Рисунок 2 Расчетная электромагнитная диаграмма

Графическими приемами, подробно рассмотренными в [2] и выполненными на поле электромагнитной диаграммы генератора рисунок 2, находим ∆Ф₁ = 50 Мкс.

Тогда

wi₁ = 16,2 А, отсюда

i₁ = 9·10^-3 А.

Напряжение на конденсаторе U_c,к  в конце каждого интервала будет равно [4]:

U_c,k  = U_c,k-1  +  dt ≈ U_c,k-1  +  (i_r-1 + i_r )·∆t                                  (11)

Тогда напряжение на конденсаторе U_c,1  в конце первого интервала будет равно:

U_c,1  = 3,5 В.

Аналогичным образом проведены расчеты остальных четырех участков. Результаты расчетов сведены в таблицу 2.

Таблица 2

	∆Фк , Мкс	wik , A	ik , A	Uk , B
1-й участок	50	16,2	9·10-3	3,5
2-й участок	175	19	10,6·10-3	7,6
3-й участок	337,5	23,9	23,9·10-3	16,8
4-й участок	525	43,7	27,3·10-3	42,9
5-й участок	1900	307,6·	170,9·10-3	120