Лабораторний практикум з курсу «Основи автоматики», страница 8

6.10 Покажіть, що в замкнутій системі, що складається з n однакових інерційних ланок першого порядку зі сталою часу Т, граничне по умові стійкості значення загального передаточного коефіцієнта розімкненого контуру не залежить від сталої часу і дорівнює

 

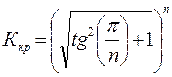
6.11 Для системи, що складається з ПІ – регулятора та інерційного об'єкту другого порядку з двома однаковими сталими часу Т₁ = Т₂, побудуйте область стійкості в площині настроювальних параметрів К_п і  К_і (Т_і).

6.12 За якими правилами визначаються еквівалентні передаточні функції для послідовного, паралельного і зустрічно – паралельного з'єднання лінійних елементів.

 ЛАБОРАТОРНА РОБОТА №5

ДОСЛІДЖЕННЯ ТОЧНОСТІ ЗАМКНУТИХ САК

 В СТАЛИХ РЕЖИМАХ

1 Мета роботи

Досліджування впливу структури ланок САК і типу зовнішньої дії на  величину похибки в усталеному режимі.

2 Короткі теоретичні відомості

Призначення автоматичної системи керування – зміна вихідної величини x(t) відповідно до зміни задаючої дії x_з(t) при будь-яких змінах задаючої і збурюючої величини. Точність системи в усталеному режимі залежить як від виду дії сигналу утворюючого похибку, так і від структури і параметрів САК, тобто від її математичного опису Ф_e(s). Якість регулювання системи в усталеному режимі характеризується значеннями коефіцієнтів похибок.

Точність САК при гармонічній дії оцінюють по значенню   - модуля КФЧХ замкнутої системи по похибці відносно відповідної зовнішньої дії, рівної відношенню амплітуди сигналу похибки ΔX_m(ω) до амплітуди зовнішньої дії А₁(ω) що викликає похибку

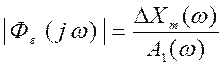                                       (2.1)

Згідно принципу суперпозиції, похибка системи складається з декількох складових. Так, наприклад, для системи, зображеної на рисунку 2.1, похибка  ε  складається з чотирьох складових

                  ε = ε_з + ε_в + ε_х + ε_п ,                                (2.2)

де ε_з – складова, обумовлена неточним відтворенням системою завдання  х_з  на виході системи;

ε_в, ε_х, ε_п – складові, обумовлені неповною компенсацією регулятором збурень y_в, x_в і завади x_п на керовану величину x. Причому кожна складова похибки пропорційна величині дії, що створила її.

 

		Рисунок 2.1

 

Знаючи передаточні функції замкнутої системи по каналах збурення – похибка:  ;  ;  ;   і зображення відповідних збурень: X_з(s); Y_в(s); U_п(s); X_в(s) можна визначити зображення похибки

E(s)= X_з(s)  + Y_в(s)  + U_п(s)  + X_в(s)  =

= Е_з(s)+ Е_в(s)+ Е_п(s)+ Е_х(s)                                   (2.3)

Узявши зворотне перетворення по Лапласу можна визначити як змінюється під час перехідного процесу кожна складова похибки ε_з, ε_в, ε_х, ε_п а також похибка системи в цілому.

Похибку в усталеному режимі, тобто після закінчення перехідного процесу, можна визначити використовуючи теорему про кінцеве значення оригіналу

,

наприклад,  e_{з уст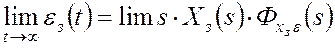}  =                  (2.4)

Похибку в усталеному режимі можна визначити також за допомогою коефіцієнтів похибок С₀, С₁, С₂ . Складова похибки від довільного х_і – го сигналу має вираз

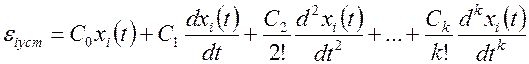
Значення коефіцієнтів визначаються за виразами

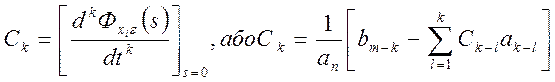 ,          (2.5)

де b і а – коефіцієнти поліномів чисельника і знаменника передавальної функції замкнутої системи   по каналу збурення – похибка, причому a_n і b_m – вільні члени цих поліномів.

3 Домашня підготовка

3.1 Визначити усталену похибку в замкнутій САК з П, ПІ, ПД і ПІД – регуляторами, зображеної на рисунку 2.1. Похибку визначати для К_р = 1 і К_р = 2, при х_з(t)= 1(t). Результати занести в таблицю 4.1. Параметри об'єкту керування Н₁(р), Н₂(р), Н₃(р) і регуляторів Н₆(р), Н₇(р), Н₈(р), Н₉(р) узяти із таблиць 2.1 і 2.2 (див. лаб. роботу № 1). Розрахунки привестиу звіті.

3.2 Визначити, використовуючи вираз (2.1), усталену похибку за завданням для замкнутої системи з П і ПД – регулятором, зображеної на рисунку 3.1, при коефіцієнті передачі регулятора К_р = 2, для x_з(t)=A₁Sinωt з частотами вхідного сигналу 50, 100 і 150 Гц. Результати занести в  таблицю 4.1. Параметри об'єкту керування і регулятора узяти із таблиць 2.1 і 2.2 (див. лаб. роботу №1). Значення А₁= узяти з умови лабораторної роботи, що U_з = 0,55 В (див. 4.4.2, 4.4.3). Розрахунки привести у звіті.

 

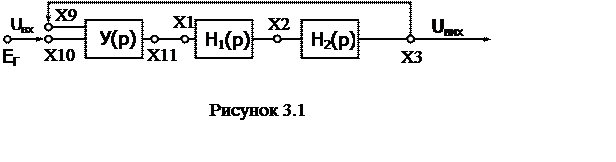4  Методичні вказівки до виконання роботи

4.1 Підготувати стенд до роботи. Натиснути кнопки «4, 5, 6» і «S5». Вольтметр встановити в режим вимірювання постійної напруги. Включити стенд, осцилограф, вольтметр.

4.2 Досліджувати точність замкненої САК в усталеному режимі при постійному сигналі на вході (статична точність), коефіцієнт підсилення регулятора – близький до одиниці.

4.2.1 Регулятор в режимі П (кнопки «S2», «S5» – натиснуті, «S1» – віджата). Встановити ручку «U_вх» в положення мінімального підсилення (крайнє праве). Подати на вхід регулятора, гніздо X9, сигнал від джерела Е₁ = 4 В. Визначити вольтметром сигнал на виході регулятора, гніздо Х11. Обчислити значення коефіцієнта підсилення регулятора К_р  і результат занести в таблицю 4.1. Перерахувати значення сигналу завдання по формулі U_з = 0,22Е₁ і занести в таблицю 4.1. При дослідженні всіх типів регуляторів сигнал завдання не змінювати.

4.2.2 Зібрати схему замкнутої САК згідно рисунку 4.1.

 

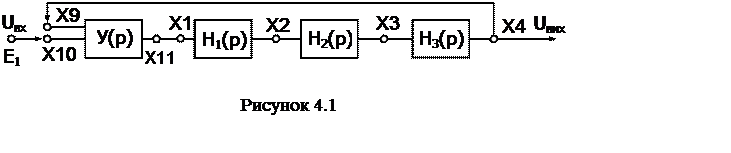4.2.3 Досліджувати САК з П - регулятором (кнопки «S2», «S5» – натиснуті, «S1» – віджата). Визначити вольтметром сигнал на виході системи, гніздо Х4, результат занести в таблицю 4.1.

4.2.4 Досліджувати САК з ПД – регулятором (кнопки «S1», «S2», «S5» – натиснуті). Визначити вольтметром сигнал на виході системи, гніздо Х4,  результат занести в таблицю 4.1.

4.2.5 Досліджувати САК з ПІ – регулятором (кнопки «S5» – натиснута, «S1», «S2» – віджаті). Визначити вольтметром сигнал на виході системи, гніздо Х4,  результат занести в таблицю 4.1.

4.2.6 Досліджувати САК з ПІД – регулятором (кнопки «S1», «S5» – натиснуті, «S2» – віджата). Визначити вольтметром сигнал на виході системи, гніздо Х4,  результат занести в таблицю 4.1.