Лабораторний практикум з курсу «Основи автоматики», страница 14

Визначити величину критичного коефіцієнта підсилення нелінійного елемента. Обертаючи ручку «U_вх» зафіксувати момент зриву автоколивань. Відключити регулятор від системи (розімкнути САК), подати на вхід регулятора (гніздо Х9) сигнал від джерела Е₁ величиною близько 0,3 В. Зміряти вольтметром постійного струму рівень вхідного (гніздо Е₁) та вихідного (гніздо Х11) сигналів регулятора. Визначити коефіцієнт підсилення К_кр та занести його значення до таблиці 4.3.

Таблиця 4.3

Тип НЕ	Параметри НЕ			Ккр		Параметри автоколивань
	b	с	Кне	Експ.	Розр.	Т, мс		А, В		ω, с
						Експ.	Розр.	Експ.	Розр.	Експ.	Розр.
Реле з гістерезисом
Ідеальне реле
Підсилювач з обмежувачем

5 Обробка результатів

5.1 Построїти статичні характеристики нелінійних ланок, визначити їхні параметри, результати занести в таблицю 4.3.

5.2 Построїти фазовий портрет для САК з НЕ типу «реле з гістерезисом» (див. рис. 4.1). Визначити амплітуду, період і частоту автоколивань, що виникають у системі. Розрахунки привести у звіті, результати занести до таблиці 4.3.

5.3 Дослідити на стійкість методом Попова САК з НЕ «підсилювач з обмежувачем» (див. рис. 4.2), коефіцієнт підсилення нелінійного елемента К_не(див. табл. 4.3). Визначити критичний коефіцієнт підсилення лінійної частини. Розрахунки привести у звіті, результати занести до таблиці 4.3.

6  Контрольні питання ТА задачі

6.1 Назвіть основні особливості нелінійних систем.

6.2 Назвіть основні види нелінійних елементів, їх математичний опис.

6.3 Наведіть приклад істотно нелінійного елемента з однозначною і неоднозначною статичною характеристикою.

6.4 Фазова траєкторія, як її вигляд пов’язаний з характером перехідного процесу, у якій системі координат строїться фазова траєкторія?

6.5 Як визначити по фазовому портрету амплітуду і частоту автоколивань в САК?

6.6 Метод гармонічного балансу.

6.7 Як визначити амплітуду і частоту автоколивань в САК методом гармонічного балансу?

6.8 Комплексний еквівалентний коефіцієнт передачі нелінійного елемента, коефіцієнти гармонічної лінеаризації.

6.9 Оцінка абсолютної стійкості нелінійних САК за допомогою критерію Попова.

6.10 Як впливає кутовий коефіцієнт К_не на стійкість системи (при незмінній лінійній частині)?

6.11 Постройте графік вихідного сигналу трипозиційного релейного елементу, на вході якого діє синусоїдальний сигнал.

ЛАБОРАТОРНА РОБОТА № 8

ДОСЛІДЖЕННЯ ІМПУЛЬСНИХ ЕЛЕМЕНТІВ

1 МЕТА РОБОТИ

Досліджування статичних характеристик імпульсних елементів із ШІМ та АІМ.

2 КОРОТКІ ТЕОРЕТИЧНІ відомості

Імпульсні та цифрові системи регулювання відрізняються від безперервних систем наявністю в каналі керування імпульсного елемента (ІЕ), що перетворює безперервну величину в послідовність імпульсів тієї ж або іншої форми. При довільному вхідному сигналі х(t) вихідний сигнал імпульсного елемента y(t) для моментів часу  описується рівнянням (2.1).

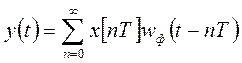,                (2.1)

де Т – період квантування імпульсного елемента; 

γТ – тривалість імпульсу;

w_ф(t – nT) – функція форми.

Імпульсний елемент, у якого функція форми представляє одиничну           δ – функцію, називають ідеальним. Його вихідна величина являє собою послідовність модульованих по «площі» δ – функцій.

Основними параметрами реального імпульсного елемента є коефіцієнт передачі К_і, період повторення Т, тривалість  γТ, амплітуда U_і і форма імпульсів. Залежність величини модульованого параметра вихідної послідовності від відповідних дискретних значень вхідної величини називається статичною характеристикою імпульсного елемента.

Для імпульсного елемента з АІМ крутизна лінійної характеристики дорівнює коефіцієнтові передачі

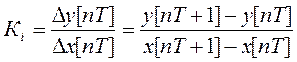                       ,            (2.2)

де x[nT] – значення вхідної величини в дискретний момент часу;

у[nТ] – відповідна йому амплітуда вихідного імпульсу.

Крутизна характеристики широтного ІЕ

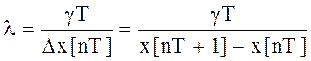                                                 (2.3)

При аналізі  систем з АІМ реальний імпульсний елемент ІЕ заміняють еквівалентним послідовним з'єднанням ідеального імпульсного елемента ІІЕ та формуючого елемента ФЕ. Структурна схема амплітудно – імпульсної САК представлена на рисунку 2.1. ІІЕ перетворює безперервний сигнал x(t) у послідовність миттєвих рівновіддалених один від одного імпульсів, площі яких пропорційні значенням вхідного сигналу в дискретні моменти часу. ФЕ або демодулятор утворює з миттєвих імпульсів такі імпульси, що за формою збігаються з імпульсами на виході реального імпульсного елемента ІЕ.

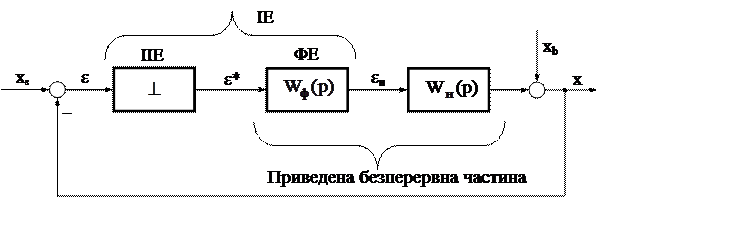
Рисунок 2.1 Структурна схема амплітудно – імпульсної САК

Формуючий елемент є ланкою безперервної дії, і його при аналізі зручно поєднувати з безперервною частиною системи (див. рис. 2.1). З'єднання, що утвориться при цьому, називається приведеною безперервною частиною системи (ПБЧ). Передаточна функція приведеної безперервної частини має вигляд

У випадку, що часто зустрічається, несучі імпульси мають прямокутну форму, тобто при амплітудно – імпульсній модуляції першого роду передаточна функція формуючого елемента має вигляд

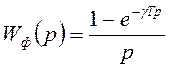                                                         (2.4)

Відносну тривалість імпульсів γ = 1 має формуючий елемент (ФЕ) з фіксацією інформації на період, який називається екстраполятором нульового порядку або фіксатором.

В САК з фіксатором дискретна передаточна функція (ДПФ) розімкнутої системи може бути визначена за формулою

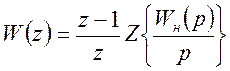
ДПФ розімкненого кола можна визначити за формулами наближеного переходу від передаточної функції безперервної частини W_н(р) (без урахування фіксатора) до ДПФ

   

або

3 ДОМАШНЯ ПІДГОТОВКА

3.1 Вивчити матеріал [3, С. 336 – 363; 4, С. 73 – 105].