Лабораторний практикум з курсу «Основи автоматики», страница 3

5.9 Що таке розімкнений контур системи і чому дорівнює його передаточна функція?

5.10 Методика отримання часових характеристик ланок.

5.11 Методика отримання частотних характеристик ланок.

5.12 Складіть аналогову модель елемента що описується диференціальним рівнянням

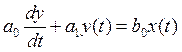
5.13 Методика аналогового моделювання лінійних САК.

ЛАБОРАТОРНА РОБОТА № 2

ДОСЛІДЖЕННЯ ЧАСОВИХ ХАРАКТЕРИСТИК

 ЛІНІЙНИХ  ЛАНОК

1 Мета роботи

Досліджування динамічних властивостей та знаходження параметрів передаточних функцій ланок за їх часовими характеристиками.

2  Короткі теоретичні відомості

            Часовою характеристикою називається закон зміни вихідної величини Y у функції часу t при нульових початкових умовах. Часові характеристики ланки залежать від властивостей ланки і від характеру зовнішньої дії, для якої вони визначаються.

В лабораторній роботі розглядаються часові характеристики ланок, які є реакцією ланок на стандартні сигнали:

– перехідна характеристика (функція) h(t) – це реакція ланки на одиничний стрибкоподібний сигнал х(t) = 1(t);

– імпульсна перехідна характеристика (функція ваги) w(t) – реакція ланки на одиничний імпульс х(t) = d(t).

Перехідна функція може бути визначена експериментально або обчислена теоретично. Якщо досліджувана ланка описується передаточною функцією W(s), то з урахуванням того, що зображення по Лапласу стрибкоподібної функції L{1(t)}=  , перехідна характеристика

                                            

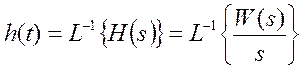
       Графік перехідної функції будується в координатах (h, t). Для лінійних ланок, при неодиничному стрибку вхідної величини Х(t) = A·1(t), вихідна величина ланки змінюватиметься згідно із законом Y(t)= A·h(t), де А = const.

Функція ваги може бути знайдена експериментально або теоретично. Для ланки з передаточною функцією W(s) з урахуванням того, що

L{δ(t)}= 1,

w(t) = L^-1 {W(s)}

Якщо на вхід лінійної ланки поступає неодинична дельта-функція         x(t) = A· δ(t), де А = const – це площа вхідного імпульсу, яка дорівнює В·с, то реакція ланки на цей імпульс дорівнює у(t) = A·w(t). Графік функції ваги строїться в координатах (w, t).

          Перехід із області зображень s в область дійсної змінної t (час) здійснюється  за  допомогою  формули  розкладання.  Наприклад,  якщо  X(s) = 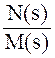 , то за відсутності кратних коренів знаменника

     x(t)=  ,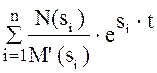

де  s_i – корені функції M(s).

За наявності кратних коренів s_k, кратності n_k

      x(t)=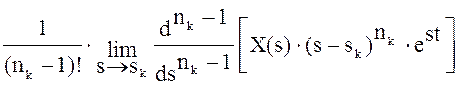  

Якщо знаменник має два однакові корені (n_k = 2), то

   x(t) =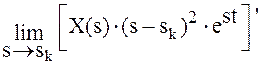

3 Домашня підготовка

3.1Вивчити матеріал [1, С. 40 – 64; 4, С. 42 – 88]. Звернути увагу на експериментальне визначення параметрів ланок: аперіодичного першого порядку  [1, С. 56; 4, С. 74,  рисунок 3.11],  коливного  [1, С. 60 – 61; 4, С. 85 – 87, рисунок 3.2 (г, д, е), формули (3.96) – (3.99)].

3.2 Використовуючи таблиці 2.1 і 2.2 (див. лаб. роботу №1):

– записати передаточну функцію аперіодичної ланки першого порядку Н₁(р), привести її схемну реалізацію. Одержати вираз для перехідної і вагової функцій. Построїти графіки перехідної і вагової функцій, привести таблицю значень;

– записати передаточну функцію аперіодичної ланки другого порядку, представлену у вигляді послідовного включення Н₁(р), Н₂(р), привести схемну реалізацію. Одержати вираз для перехідної і вагової функцій. Построїти графіки перехідної і вагової функцій, привести таблицю значень;

– записати передаточну функцію коливної ланки Н₄(р) і привести схемну реалізацію. Одержати вираз для перехідної і вагової функцій, построїти графіки, привести таблицю значень.

Примітка. При викреслюванні графіків часових характеристик масштаб по вертикальній осі прийняти рівним (0,1 – 0,2) . По горизонтальній осі (час t) масштаб узяти рівним (0,25 – 0,50)  - для ланок Н₁(р) і Н₁(р) · Н₂(р), і рівним (0,5 – 1,0)  - для коливної ланки Н₄(р).

4  Методичні вказівки До виконання роботи

4.1 Натиснути кнопку «4,5,6» перемикача лабораторних робіт і  кнопку «I-II» перемикача вимірювальних кіл. Включіть стенд, осцилограф.

4.2 Підключити один із входів осцилографа до гнізда 1(t), зарисувати осцилограму стрибкоподібного сигналу 1(t) і занести його рівень U_вх в таблиці 4.1 і 4.2.

4.3 По черзі  подати сигнал  1(t)  на ланки  Н₁(р),  Н₁(р) · Н₂(р),  Н₄(р), зарисувати осцилограми на виході цих ланок. Всі (чотири) осцилограми розташувати одну під одною, синхронізуючи їх за часом з вхідним сигналом. При знятті осцилограм сигнал подають на обидва канали осцилографа, при цьому на перший канал подається вхідний сигнал, на другий – вихідний. Для зручності осцилографування перемикачем полярності другого входу осцилографа встановити сигнали які спостерігаються на обох каналах одного знаку. Масштаби  для  всіх  осцилограм  узяти  однакові: по підсиленню – в межах 1 В/см; за часом – в межах 1 мс/см. Занести в таблиці 4.1 і 4.2 стале значення сигналу U_ст і час перехідного процесу t_п.п. В таблицю 4.2 занести значення періоду коливань Т_к і амплітуд двох сусідніх коливань U_m1 і U_m2 відносно сталого значення.

4.4 Підключити один із входів осцилографа до гнізда d(t), зарисувати осцилограму імпульсного сигналу δ(t), зміряти його рівень U_імп і тривалість Т_імп. Визначити площу імпульсного сигналу S_вх і занести в таблиці 4.1 і 4.2.

4.5 По  черзі  подати  сигнал δ(t) на ланки  Н₁(р), Н₁(р) · Н₂(р),  Н₄(р), зарисувати осцилограми на виході цих ланок, розташувати їх як вказано в пункті 4.3. Масштаб по підсиленню вибрати в межах 0,1 В/см, за часом – 1 мс/см. Занести в таблицю 4.1 найбільше значення вихідного сигналу U_m (при t = 0) і час перехідного процесу t_п.п. В таблицю 4.2 занести значення амплітуд двох сусідніх коливань U_m1 і U_m2, періоду коливань Т_к і часу перехідного процесу t_п.п.

Таблиця 4.1 –  Експериментальне  дослідження  аперіодичної

                          ланки першого  порядку  Н₁(р)

Перехідна характеристика			Імпульсна характеристика
Вхідний сигнал	Вихідний сигнал		Вхідний сигнал			Вихідний сигнал
Uвх, В	Uст, В	tп.п., с	Uімп, В	Тімп, с	Sвх, В·c	Um, В	tп.п., с