Лабораторний практикум з курсу «Основи автоматики», страница 4

Таблиця 4.2 – Експериментальне дослідження коливної

                         ланки   Н₄(р)

Перехідна характеристика						Імпульсна характеристика
Вхідний сигнал	Вихідний сигнал					Вхідний сигнал	Вихідний сигнал
Uвх, В	Uст, В	Um1, В	Um2, В	Тк, с	tп.п., с	Sвх, В·c	Um1, В	Um2, В	Тк, с	tп.п., с

Таблиця  4.3  –  Розрахунок  параметрів  аперіодичної  ланки

                            першого  порядку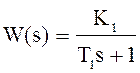   

Перехідна характеристика				Імпульсна характеристика
Дані після  нормування		Параметри ланки		Дані після  нормування		Параметри ланки
К1	Т1, с	К1	Т1, с	Т1, с		К1	Т1, с

Таблиця 4.4  –  Розрахунок   параметрів   коливної   ланки

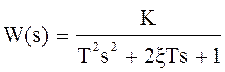                     по її перехідній характеристиці

Дані після нормування				Проміжні дані			Параметри ланки
К	А1	А2	Тк, с	ωκ, с-1	β	ω0, с-1	К	Т, с	ξ

Таблиця  4.5  –  Розрахунок   параметрів   коливної   ланки

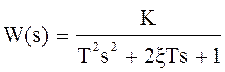                     по її імпульсній характеристиці

Дані після нормування			Проміжні дані			Параметри ланки
А1	А2	Тк, с	ωκ, с-1	β	ω0, с-1	Т, с	ξ

5  Обробка результатів

5.1 Привести експериментальні графіки вхідних сигналів, перехідних та імпульсних характеристик досліджуваних ланок. Графіки для пунктів 4.2 і 4.3 привести на одному листі, для пунктів 4.4 і 4.5 – на іншому. Провести нормування часових характеристик, для чого необхідно ординати вихідного сигналу розділити на рівень вхідного сигналу – при отриманні перехідної характеристики і на площу вхідного імпульсу – при отриманні вагової функції.

5.2 Використовуючи перехідну та імпульсну характеристики аперіодичної ланки першого порядку, визначити її параметри, результати занести в таблицю 4.3.

5.3 Використовуючи перехідну та імпульсну характеристики коливної  ланки, визначити її параметри, результати занести в таблиці 4.4 і 4.5.

При обробці результатів експерименту використовуються вирази із джерел, вказаних в пункті 3.1:

ω_κ =   ;        β = 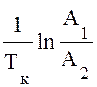 ;        ω₀ =  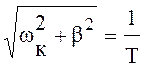;        ξ = β · Т

5.4 Розрахунки привести у звіті.

5.5 Порівняти розрахункові (див. розділ 3) і експериментальні (див. таблиці 4.3, 4.4, 4.5) значення параметрів ланок. Результати занести в таблицю 5.1.

Таблиця 5.1

Експеримент

Розрахунок

Першого порядку

Коливна

Першого порядку

Коливна

Перехідна характеристика

Імпульсна характеристика

Перехідна характеристика

Імп. характеристика

Перехідна характеристика

Імпульсна характеристика

К1

Т1, с

К1

Т1, с

К

Т,с

ξ

Т,с

ξ

К1

Т1,с

К

Т,с

ξ

6  Контрольні питання ТА задачі

6.1 Пряме перетворення Лапласа, область його вживання.

6.2 Зворотне перетворення Лапласа, область його вживання.

6.3 Часові характеристики, перехідна та вагова функції.

6.4 Методика   експериментального   визначення   перехідної    характеристики  ланки.

6.5 Методика експериментального визначення вагової (імпульсної) характеристики ланки.

6.6 Інтегруюча ланка, її передаточна функція, перехідна і вагова характеристики.

            6.7 Диференціююча ланка, її передаточна функція, перехідна і вагова характеристики.

            6.8 Аперіодична ланка першого порядку, її передаточна функція, перехідна і вагова характеристики.

            6.9 Коливна ланка, її передаточна функція, перехідна і вагова характеристики.

6.10 Аперіодична ланка другого порядку, її передаточна функція, перехідна і вагова характеристики.

6.11 Методика отримання перехідної і вагової характеристик по відомій передаточній функції ланки.

6.12 Методика визначення типу ланки і значень її динамічних параметрів по експериментальним часовим характеристикам.

ЛАБОРАТОРНА РОБОТА №3

 ДОСЛІДЖЕННЯ ЧАСТОТНИХ ХАРАКТЕРИСТИК

 ЛІНІЙНИХ ЛАНОК

1 Мета роботи

Досліджування динамічних властивостей та знаходження параметрів передаточних функцій ланок по їх частотним характеристикам.

2  Короткі теоретичні відомості

          Якщо на вхід лінійної ланки подати гармонічний сигнал х(t)=X_msinωt, то на виході ланки матимемо гармонічний сигнал тієї ж частоти у(t) = Y_msin(ωt+φ). При цьому амплітуда і фаза вихідного сигналу залежить від властивостей ланки, амплітуди і частоти вхідного сигналу.

          Залежність амплітуди А(ω) і фази φ(ω), між вхідним і вихідним сигналами, від частоти називається частотними характеристиками ланки. Для визначення сталої реакції ланки на гармонічний сигнал достатньо знати комплексну фазочастотну функцію W(jω), яку одержують заміною в передаточній функції W(s) змінної s на jω. Κомплексна фазочастотна характеристика (КФЧХ) може бути представлена в декількох видах. Так, наприклад, в показовій формі

                                                    W(jω)=А(ω)e^jφ(ω) ,                                    

де А(ω)=|W(jω)|;  

φ(ω)=argW(jω)

          або у вигляді

                                                   W(jω)=U(ω)+jV(ω) ,                                                 

де   U(ω)=ReW(jω);     

V(ω)=ImW(jω)