Лабораторний практикум з курсу «Основи автоматики», страница 6

Коливна ланка Н₄(р)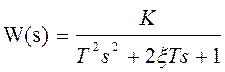    

Таблиця 4.3

Домашня  підготовка	f, Гц	0	50	100		150	200	300	400
	ω, с-1
	А
	φ, град
	Lm, дБ
Експеримент	U1, В
	U2, В									max
	α, град				270
	φ=(1800-α), град				- 90
	А=U2/U1
	Lm=20lgA, дБ
	δφ,  %
	δА, %

5 Обробка результатів

5.1 Нанести експериментальні значення точок частотних характеристик, використовуючи результати вимірювань наведені в таблицях 4.1, 4.2 і 4.3, на графіки, отримані при домашній підготовці. Визначити похибки δφ і δА, значення похибок занести в таблиці.

5.2 Визначити по експериментальним значенням частотних характеристик (див.табл. 4.1 – 4.3) динамічні параметри досліджуваних ланок, використовуючи для цього аналітичні вирази АЧХ і ФЧХ відповідних ланок. Результати розрахунків привести в звіті. Доцільно використовувати вирази АЧХ і ФЧХ у вигляді:

  ,       ;

    ,  ;

    ,  

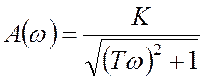
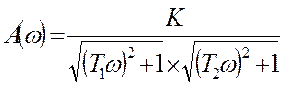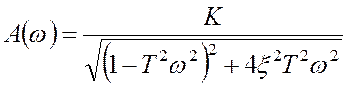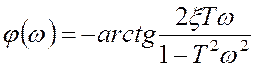
5.3 Порівняти значення динамічних параметрів ланок, одержаних за даними експерименту, зі значеннями, одержаними розрахунковим шляхом за даними таблиць 2.1 і 2.2 (див.лаб.роботу№1). Результати занести в таблицю 5.1.

Таблиця 5.1

	Аперіодична ланка 1-го порядку		Аперіодична ланка 2-го порядку			Коливна ланка
	К	Т, с	К	Т1, с	Т2, с	К	Т, с
Експеримент
Розрахунок
Похибка, %

6  Контрольні питання ТА задачі

6.1 Частотні характеристики ланок (КФЧХ, АЧХ, ФЧХ).

6.2 Методика експериментального визначення частотних характеристик.

6.3 Інтегруюча ланка та її частотні характеристики.

6.4 Диференціююча ланка та її частотні характеристики.

6.5 Аперіодична ланка першого порядку та її частотні характеристики.

6.6 Коливна ланка та її частотні характеристики.

6.7 Методика отримання частотних характеристик ланки по її передаточній функції.

6.8 Методика визначення типу ланки та її динамічних параметрів по експериментально знятій КФЧХ.

6.9 Побудувати КФЧХ ланки якщо відоме її диференціальне рівняння:

а)    ;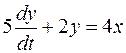

б)    ;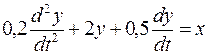

в)    ;

г)    .  

6.10 Визначте для ланки чистого запізнювання з t = 10 с фазовий зсув і амплітуду вихідного сигналу при подачі на її вхід синусоїдального сигналу x = 50 sin 2t.

6.11 Як впливає безінерційна ланка на амплітуду і фазу синусоїдального вхідного сигналу?

6.12 Приведіть основні формули які зв'язують КФЧХ, АЧХ і ФЧХ між собою.

ЛАБОРАТОРНА РОБОТА № 4

 СТІЙКІСТЬ ЛІНІЙНИХ САК

1 Мета роботи

Досліджування впливу параметрів і структури ланок на стійкість лінійних САК.

2 Короткі теоретичні відомості

Стійкість – це властивість САК повертатися в заданий або близький до нього сталий режим після всякого виходу з нього в результаті якої-небудь дії. Нестійка САК непрацездатна.

Стійкість визначається рішенням однорідного диференціального рівняння лінеаризованої системи, для чого необхідно визначити корені її характеристичного рівняння. Для стійкості лінійної САК необхідно і достатньо, щоб всі корені розташовувалися зліва від уявної осі площини коренів, тобто щоб дійсні частини коренів характеристичного рівняння були негативними. Перетворення стійкої системи в нестійку відбудеться в тому випадку, коли хоча б один дійсний корінь або пара комплексних коренів перейде з лівої напівплощини в праву.

Наявність коренів на уявній осі означає, що система знаходиться на межі стійкості і має  критичне значення коефіцієнта підсилення К_кр (коливна межа стійкості).

В ТАК розроблені непрямі ознаки, названі критеріями стійкості, які дозволяють судити про стійкість САК, не вирішуючи її характеристичного рівняння, зокрема, частотні критерії Найквіста і Міхайлова. Критерій Найквіста розглядає годограф КФЧХ розімкненої системи W(j), який може бути одержаний як аналітично, так і експериментально. Для стійкості замкнутої системи необхідно, щоб годограф W(j) (при зміні   від нуля до безкінечності) не охоплював точку (–1; j0). На рисунку 2.1 показана функціональна схема замкнутої САК. Годограф W(j) розімкненої системи, відповідний стійкій замкнутій системі показаний на рисунку 2.2.    

 

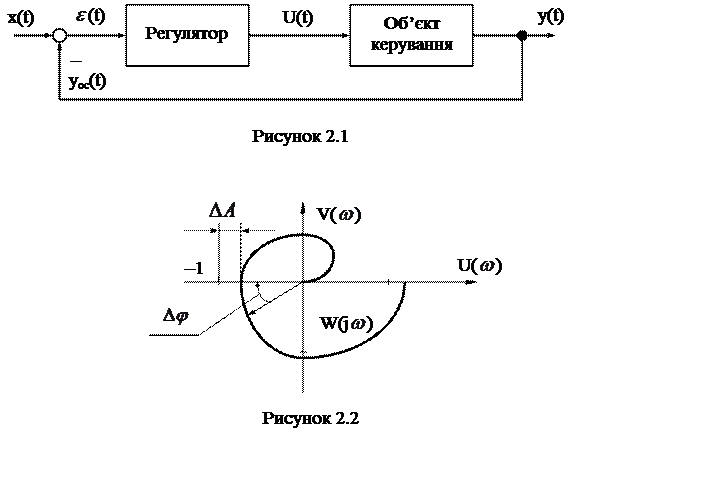Запас стійкості по модулю А і фазі  визначається віддаленістю КФЧХ розімкненої системи від точки (–1; j0). Проходження КФЧХ через точку (–1; j0) означає, що САК знаходиться на коливній межі стійкості, отже частоту автоколивань _кр та значення критичного коефіцієнта підсилення К_кр можна визначити за умов:

(_кр) = ––  і   |W(j_кр)| = 1  або  V (_кр) = 0  і  U (_кр) = – 1,

де V (_кр) – уявна частина КФЧХ розімкненої системи;

U (_кр) – дійсна частина КФЧХ розімкненої системи.