ОБОЛОЧЕЧНОГО ТИПА
Часть 1
Москва – 2002
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Курс "Методы и алгоритмы расчетов на прочность в САПР" изучается студентами специальности 220300 в течение 5 и 6 семестров. Теория тонкостенных оболочек вращения является одним из разделов этого курса и изучается в 5 семестре. В процессе изучения этого раздела студенты выполняют расчетно-проектировочную работу по расчету сосудов. Настоящая методическая разработка составлена применительно к выполнению этой работы. Теория и основы расчета оболочек вращения излагаются на лекциях и практических занятиях по курсу в достаточно полном объёме. Поэтому здесь мы ограничиваемся сводкой основных понятий теории оболочек, краткими указаниями и пояснениями отдельных вопросов и основное внимание сосредотачиваем на решении конкретных задач.
При изучении основ расчета тонкостенных оболочек вращения студент должен обратить внимание на следующие вопросы:
1. Обычно
оболочку относят к тонким при 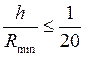 , где
, где
![]()
Эта оценка
условная, ориентировочная и зависит от степени погрешности расчета, принятой в
качестве допустимой. Оболочку с большей величиной отношения ![]() тоже можно рассматривать как тонкостенную, но при
этом следует иметь в виду, что погрешность расчета возрастает вместе с
величиной этого отношения. На практике теорию тонких оболочек иногда применяют
и при величинах отношения
тоже можно рассматривать как тонкостенную, но при
этом следует иметь в виду, что погрешность расчета возрастает вместе с
величиной этого отношения. На практике теорию тонких оболочек иногда применяют
и при величинах отношения 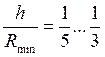 .
.
2. Необходимо тщательно проработать постановку задачи о расчете оболочек, уяснить при этом физический смысл принятых допущений. При изучении условий возникновения в оболочке безмоментного напряженного состояния обратите внимание на условия закрепления края оболочки.
3. Обратите внимание на размерности внутренних усилий в оболочке и внешних моментной и радиальной нагрузок. Все эти усилия равномерно распределены но окружности. Рассматриваются их величины, приходящиеся на единицу длины окружности.
4 Студент должен хорошо усвоить правило знаков для радиальных и угловых перемещений. Радиальное перемещение считается положительным, если сопровождается увеличением радиуса параллельного круга. Угол поворота нормали к срединной поверхности оболочки будем считать положительным, если нормаль поворачивается как показано на рис.9.
5. Основная трудность при расчете оболочек по безмоментной теории заключается в правильной записи уравнения равновесия зоны оболочки, в частности, в определении осевой равно действующей внешней нагрузки. При составлении уравнения равновесия зоны силы взаимодействия между оболочкой и средой могут рассматриваться как внешние по отношению к оболочке. В этом случае записывается уравнение равновесия собственно оболочки, и осевая равнодействующая внешней нагрузки определяется интегралом (5), стр.14.
Можно также рассматривать равновесие оболочки вместе с содержащейся в ней жидкостью. Силы взаимодействия между оболочкой и жидкостью в этом случае являются внутренними и в уравнение равновесия не входят.
Студент должен хорошо усвоить, по крайней мере, один из этих способов составления уравнения равновесия зоны. Для этого необходимо внимательно рассмотреть решение задачи, выполненное в п.п. 6 и 7 настоящего пособия.
При выполнении расчетно-проектировочной работы допускается определять численные значения напряжений и перемещений только на границах элементов сосуда. При построении графиков точки, соответствующие найденным значениям, соединяются кривыми, характер которых определяется по их уравнениям.
В 1 части настоящего пособия основное внимание уделяется расчету оболочек по безмоментной теории. Вторая часть посвящена расчету сопряжений оболочек различной геометрической формы методами моментной теории. В приложении к разработке приведены формулы для расчета длинных цилиндрических, конических и сферических оболочек.
ОБОЗНАЧЕНИЯ
R1, R2 – главные радиусы кривизны, мм;
r – радиус параллельного круга, мм;
h – толщина оболочки, мм;
m – моментная нагрузка, равномерно распределенная по окружности, Н*мм/мм;
P – радиальная нагрузка, равномерно распределенная по окружности, Н/мм;
q – распределенная по площади нагрузка, МПа;
Ns – нормальное меридиональное усилие, Н/мм;
Nt – нормальное кольцевое усилие, Н/мм;
Ms – меридиональный изгибающий момент, Н*мм/мм;
Mt – кольцевой изгибающий момент, Н*мм/мм;
Q – поперечное усилие, Н/мм;
ss – нормальное меридиональное напряжение, МПа;
st – кольцевое меридиональное напряжение, МПа;
D – радиальное перемещение, мм;
u – угол поворота нормали к срединной поверхности оболочки, рад;
ss*, st* – нормальные меридиональные и кольцевые напряжения, вычисленные по безмоментной теории, МПа;
D*, u* – радиальное и угловое перемещения, вычисленные по безмоментной теории;
Pz – осевая равнодействующая внешней нагрузки на оболочку, Н;
E – модуль упругости материала оболочки, МПа;
m – коэффициент Пуассона материала оболочки.
СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ …………………………………………………… 5
2. ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ПО ГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ ………..5
3. ОСНОВЫ ТЕОРИИ ТОНКОСТЕННЫХ ОБОЛОЧЕК ВРАЩЕНИЯ. ПОСТАНОВКА ЗАДАЧИ …………………………………………………………………………………………… 6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.