Рассмотрим более подробно этот способ, применив его для решения предыдущей задачи. При расчете сферической оболочки отсечем, как и ранее, часть ее нормальным коническим сечением с углом 2j при вершине и рассмотрим равновесие этой части оболочки вместе с заключенной в ней жидкостью, которую отделим от остальной среда плоскостью, перпендикулярной оси вращения. Расчетная схема представлена на рис. 17.
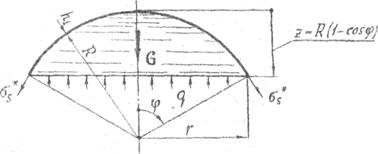
Рис.17, Расчетная схема сферической оболочки
На жидкость в рассматриваемой части сферической оболочки действует давление среды q. Величина этого давления:
.
(53)
В уравнении равновесия следует учесть также вес жидкости, заполняющей рассматриваемый сферический сегмент. Этот вес определяется формулой:
G = gV , (54)
где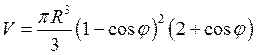 
- объём
сферического сегмента. (55)
Проектируя на ось z все силы, действующие на рассматриваемую зону оболочки и заключенную в ней жидкость, получим следующее уравнение
.
(56)
Подставляя в уравнение (56) выражения (53) – (55), получим после несложных преобразований:
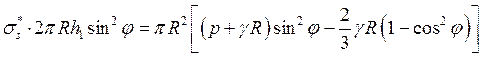. (57)
Правая часть уравнения (57) совпадает с выражением (14) для осевой равнодействующей Pz сф. Следовательно, выражение для меридионального напряжения ss*, полученное из уравнения (57), совпадет с полученным ранее выражением (15).
При
расчете цилиндрической оболочки отделяем часть сосуда вместе с жидкостью плоскостью,
перпендикулярной оси вращения. Расчетная схема для 1 участка цилиндрической оболочки
представлена на рис.18.
Воздействие отброшенной части среды на жидкость, заполняющую рассматриваемую часть сосуда, определяется давлением
.
(58)
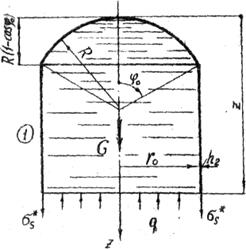
Рис.18. Расчетная схема цилиндрической оболочки
(1 участок)
Уравнение равновесия отсеченной части сосуда с жидкостью:
, (59)
где G = gV – вес жидкости, заполняющей отсеченную часть сосуда,
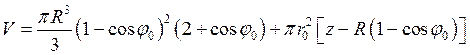– (60)
– объём отсеченной части сосуда.
Из уравнения (59) находим выражение для ss* , совпадающее с выражением (36) , полученным ранее, (убедитесь в этом самостоятельно !).
На
рис.19 представлена расчетная схема второго участка цилиндрической оболочки 
.
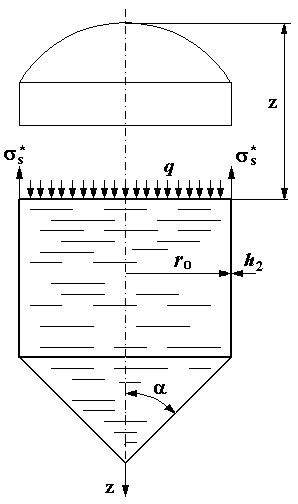
Рис.19. Расчетная схема цилиндрической оболочки
(2 участок)
Величина давления q определяется выражением (58). Уравнение равновесия отсеченной части сосуда с жидкостью
,
(61)
где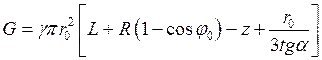 
– (62)
– вес жидкости, заполняющей отсеченную часть сосуда.
Выражение для меридионального напряжения ss*, полученное из уравнения (61), совпадает с выражением (37) (проверьте самостоятельно !)
При расчете конической оболочки отсечем, как и ранее, часть ее нормальным коническим сечением с углом 2j при вершине и рассмотрим равновесие этой части вместе с жидкостью. Расчетная схема представлена на рис.20.
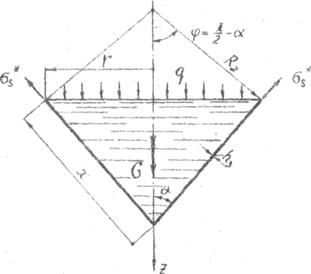
Рис.20. Расчетная схема конической оболочки
Величина давления q на жидкость, заполняющую рассматриваемую часть оболочки, определяется выражением (22).
Уравнение равновесия отсеченной части сосуда:
, (63)
где G = gV – вес жидкости,
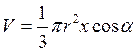– (64)
– обьём жидкости.
Из уравнения (63) находим выражение для меридионального напряжения, которое совпадает с полученным ранее выражением (26), (проверьте самостоятельно)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.