Расчет тонкостенных конструкций оболочечного типа. Часть 1: Методические указания (Основы теории тонкостенных оболочек вращения. Расчет оболочек вращения по безмоментной теории), страница 2

4. ВНУТРЕННИЕ УСИЛИЯ И НАПРЯЖЕНИЯ В ОБОЛОЧКЕ …………………………………..7

5. РАСЧЕТ ОБОЛОЧЕК ВРАЩЕНИЯ ПО БЕЗМОМЕНТНОЙ ТЕОРИИ ………………………..8

6. ПРИМЕР РАСЧЕТА СОСУДА ПО БЕЗМОМЕНТНОЙ ТЕОРИИ ………………………….....11

6.1. Сферическая оболочка ……………………………………………………………………… 11

6.2. Коническая оболочка ……………………………………………………………………….. 13

6.3. Цилиндрическая оболочка …………………………………………………………………..15

7. К  ВОПРОСУ О  РАСЧЕТЕ МЕРИДИОНАЛЬНЫХ НАПРЯЖЕНИЙ ………………………..19
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Под оболочкой понимается тело, одно из измерений которого – толщина – значительно меньше двух других. Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, носит название срединной поверхности.  Осесимметричными или просто симметричными оболочками (оболочками вращения.) называются такие, срединная поверхность которых представляет собой поверхность вращения (рис.1).

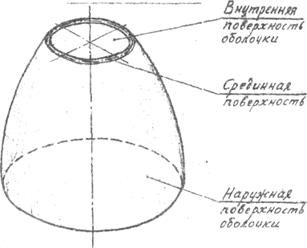
Рис 1. Тонкостенная оболочка вращения

В дальнейшем будем рассматривать осесимметричные оболочки постоянной толщины, малой по сравнению с размерами оболочки. Полагаем при этом, что нагрузка, действующая на оболочку, также осесимметрична. Для таких оболочек задача расчета значительно упрощается вследствие того, что возникающие в оболочке внутренние усилия и перемещения изменяются только вдоль образующей, оставаясь неизменными в окружном направления.

2. ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ПО ГЕОМЕТРИИ

ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ

Плоская кривая, вращением которой вокруг некоторой оси образована поверхность, называется образующей, точки пересечения ее с осью вращения – полюсами. Кривая, образованная на поверхности сечением ее плоскостью, проходящей через ось, называется меридианом. Очевидно, меридианы совпадают с образующими. Плоскости, перпендикулярные оси вращения, пересекают поверхность по окружностям, называемым параллельными кругами.

Проведем нормаль  n–n к поверхности в некоторой ее точке Р   (рис.2). Связка плоскостей, проходящих через нормаль, пересекает поверхность по линиям, называемым нормальными сечениями. Радиусы кривизны этих сечений в точке Р  будут в общем случае различны.

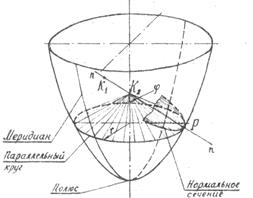
Рис.2. Поверхность вращения

Очевидно, меридиан поверхности также является нормальным сечением. Меридиан и нормальное сечение  поверхности плоскостью, перпендикулярной меридиану (перпендикулярной касательной к меридиану в точке Р), отличаются тем, что из всех нормальных сечений в данной точке они имеют наибольший и наименьший радиусы кривизны.

Радиус кривизны меридиана называется первым главным радиусом кривизны R₁ поверхности в данной точке (отрезок нормали К₁Р на рис.2), радиус кривизны нормального сечения плоскостью, перпендикулярной меридиану, –  вторым главным радиусом кривизны R₂ поверхности в этой точке (отрезок нормали К₂Р между точкой Р и осью вращения поверхности на рис.2. Центры кривизны К₁ и К₂ лежат на нормали к поверхности в этой точке, причем второй центр кривизны К₂ поверхности вращения лежит на оси вращения, как это доказывается в дифференциальной геометрии.

Нормали, проведенные к поверхности в точках параллельного крута, пересекаются в одной точке, лежащей на оси вращения, и образуют коническую поверхность, нормальную к рассматриваемой поверхности.

Радиус параллельного круга r связан со вторым главным радиусом кривизны очевидным соотношением:

,                                                                      (1)

где (  -  угол между нормалью к поверхности и осью вращения).

Теперь можно дать более точное определение понятию тонкой оболочки. Тонкостенными считаются оболочки, для которых выполняется соотношение 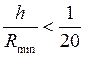,  где h - толщина оболочки, R_min = min(R₁, R₂).

В теории оболочек доказывается, что относительная погрешность расчета не превышает величины .  Поэтому, принимая указанное выше соотношение, мы обеспечиваем обычную для технических задач точность расчета.