Расчет тонкостенных конструкций оболочечного типа. Часть 1: Методические указания (Основы теории тонкостенных оболочек вращения. Расчет оболочек вращения по безмоментной теории), страница 4

5. РАСЧЕТ ОБОЛОЧЕК ВРАЩЕНИЯ ПО БЕЗМОМЕНТНОЙ ТЕОРИИ

Задача о расчете оболочек вращения наиболее просто решается в том случае, когда возможно принять, что напряжения, возникающие в оболочке, постоянны по ее толщине, и, следовательно, изгиб оболочки отсутствует, т.е. . Теория оболочек, построенная в этом предположении, называется безмоментной теорией.

Можно показать, что при    поперечная сила Q обращается в нуль. В этом случае в нормальных сечениях оболочки действуют только нормальные усилия N_s и N_t , которые могут быть определены из условий равновесия элемента оболочки.

Безмоментное напряженное состояние возникает в оболочке в том случае, когда оболочка не имеет резких переходов и жестких защемлений и, кроме того, не нагружена сосредоточенными силами и моментами. При наличии же перечисленных особенностей в местах крепления оболочки, резких изменений формы и местах приложения сосредоточенной нагрузки возникают повышенные напряжения изгиба. Более детальное исследование показывает, что этот изгиб носит местный характер, на достаточном удалении от перечисленных особых областей устанавливается безмоментное напряженное состояние (рис.7), и для расчета оболочки может быть применена безмоментная теория.

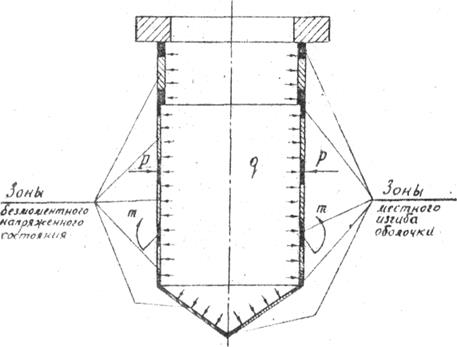
Рис.7. Зоны местного изгиба

и безмоментного напряженного состояния оболочки

Для определения напряжений в зонах местного изгиба и границ этих зон следует привлекать более точные (и более сложные!) методы моментной теории оболочек.

Будем полагать, что оболочка нагружена нормальным давлением, равномерно распределенным по поверхности оболочки или плавно меняющимся вдоль меридиана, края оболочки свободны от защемлений, так что их поворот и перемещение по нормали не стеснены, толщина оболочки постоянна. Выполнение этих условий обеспечивает практически безмоментное напряженное состояние оболочки и позволяет применение методов безмоментной теории,

Основными уравнениями безмоментной теории оболочек для определения напряжений являются:

- уравнение Лапласа

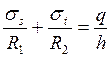                                                                            (3)

где R₁ и R₂ - главные радиусы кривизны оболочки, h - толщина оболочки;

- уравнение равновесия зоны оболочки, ограниченной параллельным кругом радиуса r:

                                                                     (4)

где  - угол между осью вращения и нормалью к оболочке не границе зоны, P_z - осевая равнодействующая внешней нагрузки на рассматриваемую часть оболочки (рис. 6).

В уравнениях (3), (4) и в последующем изложении значком * помечены величины, относящиеся к безмоментному напряженно-деформированному состоянию.

Рассматриваемая зона отделяется от оболочки нормальным коническим сечением с углом  при вершине, как показано на рис.8. Равнодействующая внешней нагрузки определяется интегралом

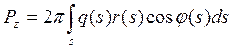                                                 (5)

В случае постоянного давления q= const выражение (5) принимает следующий простой вид:

,                                                                    (6)

т.е. равнодействующая сил постоянного давления численно равна произведению величины давления на площадь проекции поверхности рассматриваемой зоны оболочки на плоскость, перпендикулярную оси вращения.

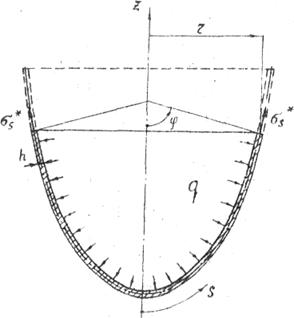
Рис.8. К условию равновесия зоны оболочки

Радиальные перемещения точек оболочки определяют на формуле:

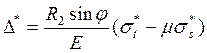                                            (7)

Угол поворота нормали к оболочке определяется выражением:

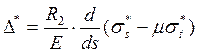                                             (8)

Положительные направления радиальных перемещения углов поворота показаны на рис.9.

Рис.9. Положительные направления радиальных перемещений и углов поворота

6. ПРИМЕР РАСЧЕТА СОСУДА ПО БЕЗМОМЕНТНОЙ ТЕОРИИ