Расчет тонкостенных конструкций оболочечного типа. Часть 1: Методические указания (Основы теории тонкостенных оболочек вращения. Расчет оболочек вращения по безмоментной теории), страница 7

,                                                         (51)

.                                                       (52)

Результаты расчета сводим в табл. 1  

Таблица 1

Результаты расчета сосуда по безмоментной теории

По результатам расчета строим эпюры меридиональных и кольцевых напряжений, радиальных и угловых перемещений для элементов сосуда, руководствуясь при этом известными из курса математического анализа правилами построения графиков кривых по их уравнениям.

На рис.15 показано распределение меридиональных и кольцевых напряжений в элементах сосуда. На рис.16 представлены эпюры радиальных и угловых перемещений.

Анализ полученных результатов приводит нас к выводу, что безмоментная теория не дает удовлетворительного решения задачи о расчете сосудов, состоящих из оболочек различной геометрической формы. Этот вывод следует из того, что в точках сопряжения элементов сосуда расчет по безмоментной теории дает нам скачки величин радиальных и угловых перемещений, 45а это противоречит условию неразрывности конструкции.

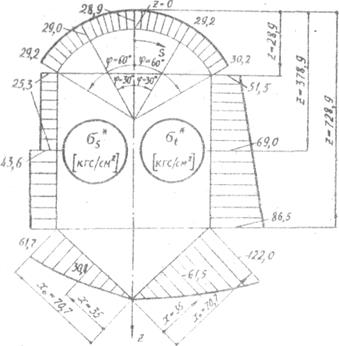
Рис.15. Графики меридиональных и кольцевых напряжений

в элементах сосуда

Полученные результаты справедливы для участков сосуда, находящихся на некотором удалении от точек сопряжения. В узких зонах элементов сосуда, примыкающих к точкам сопряжения, а также к кольцевой опоре, возникает моментное напряженное состояние, которое носит название краевого эффекта. Исследование напряженно-деформированного состояния в зонах краевого эффекта необходимо выполнять методами моментной теории оболочек.

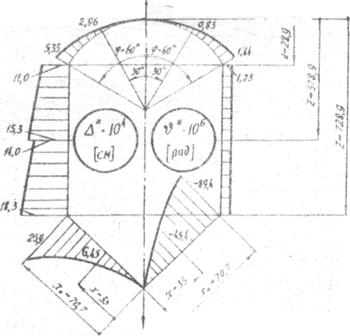
Рис.16. Графики радиальных и угловых перемещений элементов сосуда

Необходимо отметить, что вершина конической оболочки является особой точкой (в окрестности вершины, в частности, -нарушается условие тонкостенности оболочки) , и исследование напряженно-деформированного состояния зона оболочки, примыкающей к вершине, следует проводить особыми методами.

7.  К  ВОПРОСУ О  РАСЧЕТЕ МЕРИДИОНАЛЬНЫХ НАПРЯЖЕНИЙ

По безмоментной теории меридиональные напряжения определяются из уравнения равновесия зоны оболочки. В уравнении равновесия зоны оболочки (б) силы взаимодействия между оболочкой и содержащейся в ней средой рассматриваются как внешние по отношению к оболочке. Уравнение равновесия зоны можно получить иным способом, рассматривая равновесие отсеченной части оболочки вместе с заключенной в ней средой. В этом случае силы взаимодействия между средой и оболочкой станут внутренними и в уравнение равновесия системы оболочка-среда не войдут.