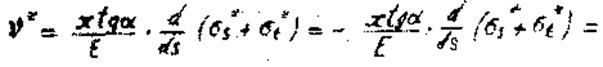Расчет тонкостенных конструкций оболочечного типа. Часть 1: Методические указания (Основы теории тонкостенных оболочек вращения. Расчет оболочек вращения по безмоментной теории), страница 6

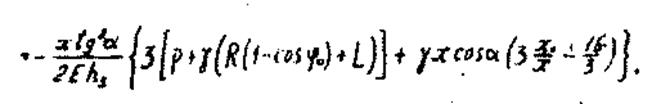                  (28)

           (28)

6.3. Цилиндрическая оболочка

Цилиндрическая оболочка нагружена переменным давлением

                                                             (29)

Координата z изменяется в пределах

Главные радиусы кривизны цилиндрической оболочки

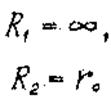                                                                 (30)

Радиус параллельного круга

r= r₀                                                                                                               (31)

При определении меридиональных напряжений следует учесть, что цилиндрическая оболочка имеет в данном случае два участка нагружения (см.рис.10):

1 участок - от сферической крышки до кольцевой опоры

2 участок - от кольцевой опоры до конического днища

Расчетная схема для 1 участка цилиндрической оболочки представлена на рис.13.

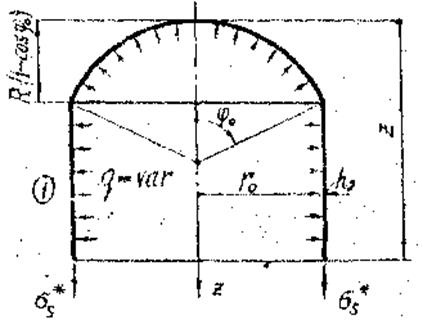
Рис.13. Расчетная схема цилиндрической оболочки (1 участок)

Уравнение равновесия рассматриваемой части сосуда:

                                                                      (32)

Осевую равнодействующую сил давления среда на сферическую крышку сосуда можно определить из выражения (14) полагая в нем j = j₀

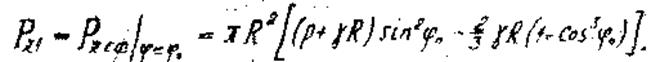           (33)

Расчетная схема для 2 участка цилиндрической оболочки представлена на рис.14

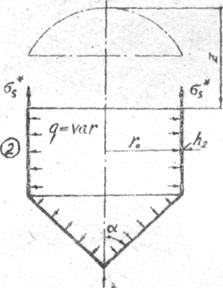
Ряо.14. Расчетная схема цилиндрической оболочки (2 участок).

Уравнение равновесия рассматриваемой части сосуда:

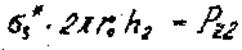                                                 (34)

где P_z2- осевая равнодействующая сил давления среды на коническое днище сосуда. Величину ее можно определить из выражения (25), полагая в нем x = x₀:

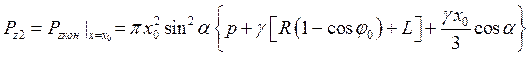                     (35)

В результате получаем следующие формулы для определения меридиональных напряжений в цилиндрической оболочке:

- на 1 участке

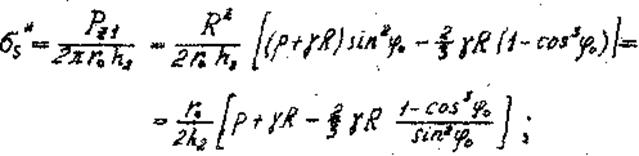          (36)

на 2 участке

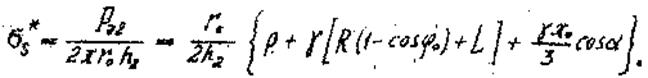           (37)

Кольцевые напряжения в оболочке находим, подставляя значения главных радиусов кривизны (30 в выражение (29) для давления q в уравнение Лапласа (3). В результате получим следующую формулу:

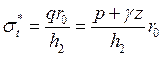,                                                                   (38)

общую для 1 и 2 участков оболочки.

Радиальные перемещения точек цилиндрической оболочки определяем по формуле (7):

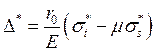
Таким образом,

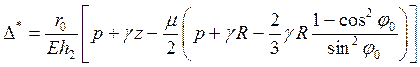  на первом участке,

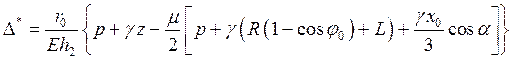  на втором участке.           (39)

Угол поворота нормали к оболочке определяем по формуле (8):

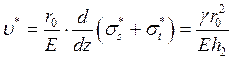                                                     (40)

Численный расчет выполним для следующих значений параметров сосуда и нагрузки:

r₀ = 500 мм,                           j₀ = 60°,                                p = 0,1 МПа,

L = 7000 мм,                          a = 45°,                                 r =1,02 кг/м³,

l  = 3500 мм,                          E = 2×10⁵ МПа,                     m = 0,3

h₁ = h₂ = h₃ = 10 мм.

Очевидно, что

,

,

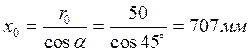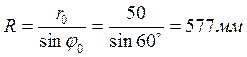g=r×g = 10^-5 Н/мм³ .

Подставляя значения параметров в выражения для напряжений и перемещений,  получаем следующие расчетные формулы для элементов сосуда:

– для сферической оболочки:

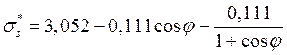,                                                (41)

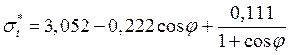,                                               (42)

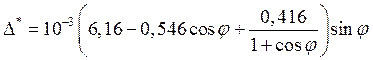,                                   (43)

.                                                                    (44)

– для цилиндрической оболочки:

  на первом участке,          

  на втором участке;                                                           (45)

,                                                                                  (46)

 на первом участке,

 на втором участке;                                (47)

;                                                                                      (48)

– для конической оболочки:

,                                                                (49)

,                                                                  (50)