Лабораторная работа № 4. Кинетостатический анализ плоских рычажных механизмов.

Лабораторная работа №4

Кинетостатический анализ плоских рычажных механизмов

         Цель работы: определение реакций в кинематических парах, мощностей и механического КПД в кривошипно-коромысловом, кривошипно-ползунном и кривошипно-кулисном механизмах.

         Оборудование: модели механизмов, измерительные инструменты, распечатки кинематических параметров, ЭВМ.

Краткие теоретические сведения

Кинетостатический анализ заключается в определении реакций в кинематических парах, мощностей и механического КПД. Полученные результаты позволят рассчитать звенья механизма на прочность, жёсткость и износостойкость. Кинетостатический анализ имеет также название "силовой расчёт". Его основные принципы:

1) Использование принципа Даламбера, когда к силам, действующим на звенья механизма, условно находящимся в равновесии, добавляют силы инерции и моменты сил инерции.

2) Использование кинематических цепей, названных группами Ассура (диадами), которые являются кинетостатически определимыми.

Задаваемые силы сопротивления F_С или моменты сил сопротивления М_С всегда направлены против движения выходного звена (против скорости v ползуна либо угловой скорости  коромысла или кулисы). Силу инерции F_и, вводимую по принципу Даламбера, прикладывают на схеме против направления ускорения центра масс.

                                      .                                            (4.1)

Направления векторов  берут из планов ускорений или из распечаток. В последнем случае приведены модули и  углы расположения векторов, отсчитанные от положительного направления оси х против часовой стрелки. Момент сил инерции М_и в Н×м равен:

                                                 ,                                         (4.2)

Он направлен против вектора углового ускорения. Вес звеньев имеет постоянное направление - вертикально вниз; его модуль в Н:

                                         ,                                           (4.3)

где g- ускорение свободного падения; g = 9,81 м/с² (можно принимать g = 10).

Силы сопротивления F_С, тяжести G, инерции F_и и моменты сил инерции М_и являются заданными, реакции в кинематических парах R и уравновешивающий момент М_у являются искомыми параметрами. Другие теоретические положения выполнения силовых расчётов рычажных механизмов приведены на примерах с числовыми данными.

А) Кривошипно-коромысловый механизм (рис. 3.1).

Графо-аналитический метод

         Пример силового расчёта кривошипно-коромыслового механизма проиллюстрирован на рис. 4.1 - 4.4. Для примера приняты следующие исходные данные:

   - из задания на кинематический анализ (см. лаб. работу №3):

угловая скорость кривошипа w₁ = 150 с^-1, длины звеньев: l_AB = 0,1 м; l_BC = 0,2 м; l_CD = 0,3 м; l_AD = 0,35 м; координаты центров масс l_BS2 = 0,4×l_BC = 0,08 м; l_DS3 = 0,3×l_CD = 0,09 м, угловая координата кривошипа j₁ = 60°;

   - результаты кинематического анализа (из распечаток к лаб. работе №3):

абсолютные скорости _В = 15 м/с; _C = 2,29 м/с; _S2 = 9,41 м/с; _S3 = 0,69 м/с;                            угловые скорости w₂ = – 71,08 с^-1; w₃ = 7,64 с^-1;            абсолютные ускорения: a_B = 2250 м/с². a_C  = 3356,86 м/с²; a_S2 = 2634,53 м/с²;

a_S3 = 1007,06 м/с²;

угловые ускорения: e₂ = 6115,53 с^-2; e₃ = 11189,37с^-2;

- исходные данные силового расчёта:

массы звеньев: m₁= 3 кг;  m₂=2 кг; m₃=5 кг;

моменты инерции звеньев: I_S2 = 0,007 кг×м²; I_S3 = 0,04 кг×м²;

момент силы сопротивления М_С = 1030 Н×м (прикладывать против направления угловой скорости w₃).

 Правило 1. Момент сил сопротивления прикладывать против направления угловой скорости звена.

Определить: реакции в кинематических парах , , , ; уравнивающий момент ; мгновенную мощность и механический коэффициент полезного действия (КПД).

1.Составление расчётной схемы диады 2-3. Диада 2-3 является кинетостатически определимой. Это означает, что не только для любого звена, но и для диады можно использовать уравнения равновесия (кинетостатики). Принцип кинетостатической определимости предполагает равенство числа неизвестных и числа уравнений равновесия. В диаде 2-3 искомыми являются  реакции R₁₂, R₂₃ и R₂₃ во вращательных кинематических парах. Они появляются после отсоединения соседних звеньев друг от друга.

         Реакция во  вращательной паре, как и в любой цилиндрической и сферической паре,  неизвестна по величине и направлению. Для решения задачи графо-аналитическим методом её раскладываем по двум направлениям: вдоль звена располагаем нормальную составляющую, ей перпендикулярно - тангенциальную. Так, в точке В диады прикладываем составляющие  и , в точке D –   и  (рис. 4.1), причём их направления принимаем произвольно, а истинное направление определяем аналитическим и графическим методами. Индексы реакции  обозначают реактивное воздействие (реакцию) на звено 2 со стороны звена 1.

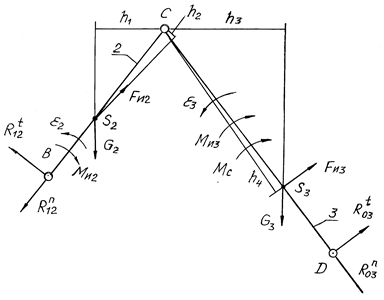
Рис. 4.1

Вес G прикладываем в центрах масс S звеньев всегда вертикально вниз. Силы инерции F_и– также в центрах масс против направления векторов линейных ускорений a_S. Моменты сил инерции М_и – против направления угловых ускорений e. Момент сил сопротивления М_С - против направления угловой скорости w₃.

2. Дополнительные исходные данные:

   - вес звеньев (направлен вертикально вниз):

    G₁ = m₁∙g = 3 ∙ 9,81 = 29 Н; G₂ = 2 ∙ 9,81 = 20 Н; G₃ = 5 ∙ 9,81 = 49 Н.

- модули сил инерции звеньев (на схеме направлять против векторов ускорений центров масс звеньев):