Структура диады 3-го вида позволяет не использовать группу Ассура, а выполнять силовой расчет более простым методом — для каждого звена в отдельности по уравнениям с одним неизвестным.
1. Вес звеньев (всегда направлен вертикально вниз) – формула (4.3):
G1 = m1g = 2 ∙ 9,81 = 20 Н; G2 = 1 ∙ 9,81 = 10 Н; G3 = 10 ∙ 9,81 = 98 Н.
2. Модули сил инерции звеньев (направлены против векторов ускорений центров масс) – формула (4.1):
Fи2 = m2aS2 = m2aB1 = 1 ∙ 22,5 = 22,5 Н; Fи3 = 10 ∙ 7,22 = 72,2 Н.
3. Модуль момента сил инерции кулисы (направлен против углового ускорения ε3) – формула (4.2):
Ми2 = IS3 ε3= 0,02 ∙ 27,67 = 0,55 Н∙м.
4. Моментное уравнение для звена 3. К кулисе 3 прикладываем заданные нагрузки и искомую реакцию R23 (рис. 4.9).
ΣМС = 0; R23∙B3C + G3h1 + Fи3h2 + (Ми3 + МС)μl = 0, (4.24)
откуда R23 = ( - G3h1 – Fи3h2 - (Ми3 + МС)μl )/ B3C .
Расчётную схему (рис. 4.9) вычерчиваем в масштабе ml = СD /lCD = 55/0,5 = 110 мм/м: СВ3 = 40 мм; h1 = 8 мм; h2 = 27 мм.
R23 = - (98∙8 + 72,2∙27 + (0,55 + 20) ∙110)/40 = - 124,8 Н.
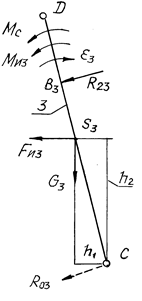
Рис. 4.9
5. Векторное уравнение для звена 3 (рис. 4.9):
(4.25)
Масштаб плана сил
mF
= 
=
36/72,2 = 0,5 мм/Н.
Длины отрезков на плане сил: 
= 124,8 ∙ 0,5 = 62,4 мм; 
= 98 ∙ 0,5 = 49 мм; 
= 36 мм. Последовательно откладываем отрезки 
в соответствии с
уравнением (4.25). На плане сил (рис. 4.10) направление реакции R23
показано противоположно изображённому на рис. 4.9, вследствие отрицательного
результата в уравнении (4.24). Искомый вектор 
получаем
замыканием векторного многоугольника. Для этого проводим отрезок из конца вектора
в начало вектора 
.
Длина отрезка = 43 мм. Реакция 
= 43/0,5 = 86 Н.
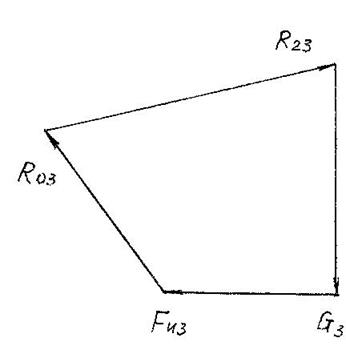
Рис. 4.10
7. Векторное уравнение для звена 2 (рис. 4.11):
.
(4.26)
Вектор 
направляем противоположно вектору 
. Длины отрезков: 
= 10∙0,5 = 5 мм; 
= 22,5∙0,5 = 11 мм. Искомый
вектор 
получаем замыканием векторного
многоугольника (рис. 4.12). Длина отрезка 
= 72
мм. Реакция 
= 72/0,5
= 144 Н.
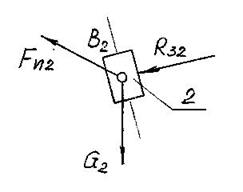
Рис. 4.11
8. Уравновешивающий момент находим по формуле (4.11) из схемы на рис. 4.13, выполненной в масштабе ml = АВ /lАB = 30/0,1 = 300 мм/м. Длина плеча h = 25 мм. Реакцию R21 прикладываем в точке B противоположно R12. Уравновешивающий момент
Му = – (R21h)/μl = – 62∙25/300 = – 5,2 Н∙м.
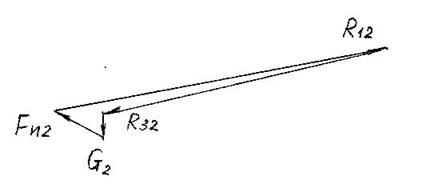
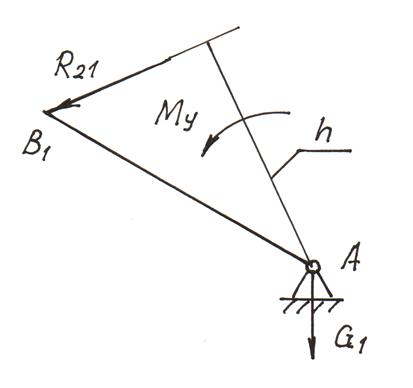
Рис. 4.13
9.
Реакцию R01 определяем из векторного треугольника по формуле (4.12). Длины отрезков 
= 72 мм; 
= 20∙0,5 = 10 мм (рис. 4.14). Искомый
отрезок 
= 75 мм. Модуль реакции R01 = 75/0,5 = 150 Н.
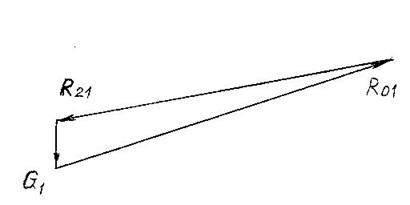
Рис. 4.14
10. Мощность сил полезных сопротивлений — формула (4.13):
Pпс = Myω1 = 5,2∙15 = 78 Вт.
11. Радиусы шарниров — формула (4.14):
мм;
мм; 
мм.
Реакции, рассчитанные для заданного положения, могут оказаться не самыми большими из 12, а радиусы шарниров могут быть заниженными. Для получения реальных радиусов их следует принимать в зависимости от длин звеньев:
r01 = 0,3lAB; r12 = 0,2lAB; r03 = 0,075lСD.
r01 = 0,3∙0,1 = 0,03 м; r12 = 0,2∙0,1 = 0,02 м;
r03 = 0,075∙0,5 = 0,0375 м.
12. Относительные угловые скорости — формула (4.15):
ω01 = |ω0 – ω1| = |0 + 15| = 15 с-1; ω12 = |ω1 – ω2| = |15 – (–2,88)| = 17,88 с-1;
ω23 = |ω2 – ω3| = |– 2,88 – 0| = 2,88 с-1;
13. Мощность сил трения:
Pт= R23 fп υВ3В2 + R01 fв ω01 r01 + R12 fвω12 r12 + R03 fп ω03 r03 = (4.27)
= 124,8∙0,1∙1,12 + 150∙0,08∙15∙0,03 + 144∙0,08∙17,88∙0,02 +
+ 86∙0,08∙2,88∙0,0375 = 24,24 Вт.
14. Мгновенная мощность — формула (4.17):
Рмгн = Рд = Рпс + Рт = 78 + 24,24 = 102,24 Вт.
15. Механический КПД — формула (4.18):
η = Рпс /Рд= 78/102,24 = 0,76
Исходные данные для анализа приведены в табл. 4.3.
Таблица 4.3. Исходные данные кривошипно-кулисного механизма
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.