Определить: реакции в
кинематических парах 
, 
, 
, 
; уравнивающий
момент 
; мгновенную мощность и механический
коэффициент полезного действия (КПД).
Решение:
1. Вес звеньев (всегда направлен вертикально вниз) – формула (4.3):
G1 = m1g = 38 ∙ 9,81 = 373 Н; G2 = 3,1 ∙ 9,81 = 30 Н; G3 = 2,2 ∙ 9,81 = 22 Н.
2. Модули сил инерции звеньев (направлены против векторов ускорений центров масс звеньев) – формула (4.1):
Fи2 = m2∙aS2 = 3,1 ∙ 3597 = 11151 Н; Fи3 = 2,2 ∙ 3713 = 8169 Н.
3. Модуль момента сил инерции шатуна (направлен против углового ускорения ε2) – формула (4.2):
Ми2 = IS2 ε2= 0,028 ∙ 5881 = 165 Н∙м.
4. Составляем расчётную схему (см. рис. 4.5).
Прикладываем в точке В искомые реакции 
и 
, в точке S2 — известные
силы G2 и Fи2, в точке С
— известные силы FС, Fи3, G3
и искомую реакцию R03, на звене 2 - момент Ми2.
Длины отрезков в масштабе ml = ВС /lBC = 72/0,3 = 240 мм/м: ВС = 72 мм; h1 = 25 мм; h2 = 50 мм.
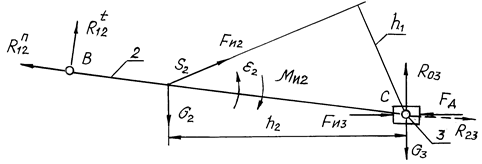
5. Составляем уравнение моментов относительно точки С — формула, аналогичная (4.4), из которой находим искомую реакцию:
= (–11151 ∙ 25 + 30,4 ∙ 50 – 165 ∙ 240)/72 = – 4401 Н.
Направление реакции — противоположно изображенному на рис. 4.5, так как получен результат со знаком «минус».
6. Масштаб плана сил — формула, аналогичная (4.7):
mF = 
= 40/8000 = 0,005 мм/Н.
7. Длины отрезков, изображающих известные векторы – формула (4.8):
= 4401 ∙ 0,005 = 22 мм;
= 30,4 ∙ 0,005 = 0,2 мм; 
=
21,6 ∙ 0,005 = 0,1 мм;
= 11151 ∙ 0,005 = 56 мм; 
=
8169 ∙ 0,005 = 41 мм.
Отрезки 
и малы и на плане сил не будут показаны.
8. Построение плана сил диады 2–3 — в соответствии с векторным уравнением:
(4.20)
4401 30 11151 22 8169 8000
Проводим отрезок 
= 22 мм (см. рис. 4.6) противоположно изображённому на рис 4.6, из его конца - отрезок 
длиной 56 мм, далее – отрезки = 41 мм
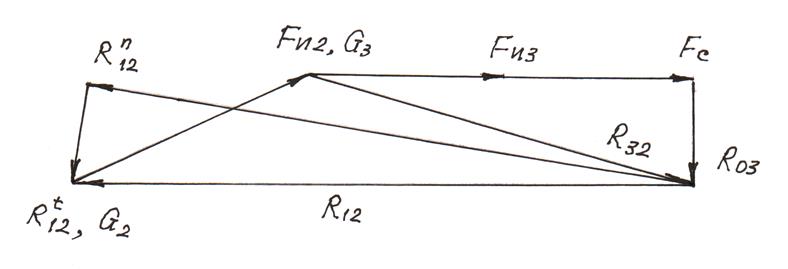
Рис. 4.6
и 
=
40мм противоположно направлению скорости 
C. Из конца отрезка проводим
перпендикулярное ему направление вектора 
, а из начала 
- перпендикулярное ему
направление вектора 
до их взаимного пересечения.
Длины отрезков:
= 22 мм; 
= 130 мм.
Модули векторов:
R03 = 22/0,005 = 4400 Н; R12 = 130/0,005 = 26000 Н.
9. Из векторного уравнения звена 2 — формула
(4.9) — на плане сил находим 
путем соединения конца
вектора с началом вектора 
.
Длина отрезка = 84 мм. Модуль реакции R32 = 84/0,005 = 16800 Н.
10. Уравновешивающий момент находим по формуле (4.11) из схемы на рис. 4.7. Отрезок АВ = lAB∙ μl = 0,08∙240 = 19,2 мм. Реакцию R21 прикладываем в точке B противоположно R12. Плечо h = 9,6 мм.
Му = (R21h)/μl = 26000∙9,6/240 = 1040 Н∙м.
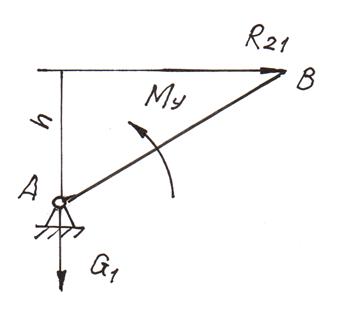
Рис. 4.7
11. Реакцию R01 определяем из векторного треугольника (рис. 4.8) по формуле (4.12). Длины отрезков в масштабе mF = 0,004 мм/Н:
=
26000∙0,004 = 104 мм; 
= 373∙0,004 = 1,5 мм.
Искомый отрезок 
= 104 мм. Модуль реакции R01 = 26000 Н.
12. Мощность сил сопротивления — формула (4.13):
Pс = Myω1 = 1040∙215 = 223600 Вт = 223,6 кВт.
Рис. 4.8
13. Радиусы шарниров — формула (4.14):
= 20,1 мм;
= 20,1 мм; 
= 16,2 мм.
Реакции, рассчитанные для заданного положения, могут оказаться не самыми большими, а радиусы шарниров могут быть заниженными. Для получения реальных радиусов их следует принимать в зависимости от длин звеньев:
r01 = 0,3lAB; r12 = 0,2lAB; r23 = 0,075lBС.
r01 = 0,3lAB = 0,3∙0,08 = 0,024 м; r12 = 0,2∙0,08 = 0,016 м;
r23 = 0,075∙0,3 = 0,0225 м.
Принимаем r01 = 0,024 м; r12 = 0,02 м; r23 =0,0225 м.
14. Относительные угловые скорости — формула (4.16):
ω01 = |ω0 – ω1| = |0 – 215| = 215 с-1; ω12 = |ω1 – ω2| = |215 – (–50,1)| = 265,1 с-1;
ω23 = |ω2 – ω3| = |–50,1 – 0| = 50,1 с-1;
15. Мощность сил трения:
Pт = R03 fп υС+R01 fв ω01 r01+R12 fв ω12 r12+R23 fп ω23 r23 = (4.21)
= 4400∙0,1∙10,6 + 26000∙0,08∙215∙0,024 + 26000∙0,08∙205,1∙0,02 +
+ 16800∙0,08∙50,1∙0,0225 = 25444 Вт = 25,4 кВт.
16. Мгновенная мощность:
Рмгн = Рс + Рт= 223,6 + 25,4= 249 кВт. (4.22)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.