Лабораторная работа № 4. Кинетостатический анализ плоских рычажных механизмов., страница 2

F_и2 = m₂∙a_S2 = 2 ∙ 2634,53 = 5269 Н; F_и3 = 5 ∙ 1007,06 = 5035 Н.

       Правило 2. Силу инерции прикладывать против направления ускорения центра масс звена.

- модули моментов сил инерции звеньев (на схеме направлять против угловых ускорений):

М_и2 = I_S2ε₂ = 0,07 ∙ 6115,53 = 428,1 Н∙м;

М_и3 = I_S2ε₂ = 0,04 ∙ 11189,37 = 447,6 Н∙м.

      Правило 3. Момент сил инерции прикладывать против направления углового ускорения звена.

В качестве расчётной схемы силового расчёта используют план положений диады в масштабе m_{l .} с нанесенными на него силами и моментами. Проводя линии действия сил G и F_и, опускают на них из точки С перпендикуляры, длины которых h_i являются плечами сил. Длины отрезков на схеме рис. 4.1 в масштабе m_l = 200 мм/м: ВС = 40 мм; СD = 60 мм; ВS₂ = 16 мм; DS₃ = 18 мм; h₁ = 15 мм; h₂ = 3 мм;h₃ = 25 мм; h₄ = 42 мм.

3. Аналитическое моментное уравнение относительно точки С для звена 2:

        ; .                                    (4.4)

Правило 4. В соответствии с принципом Даламбера в аналитическое уравнение включены силы инерции и моменты сил инерции.

   Правило 5. Знаки моментов принимать: плюс – при направлении против часовой стрелки, минус – по часовой стрелке.

Из уравнения (4.4) находим составляющую :

= (20∙15 + 5269∙3 – 428,1∙200)/40 = - 1738 Н.

В данном примере фактическое направление составляющей реакции  противоположно изображённому на схеме.

4. Аналитическое моментное уравнение относительно точки С для звена 3:

;                                      (4.5)

Из уравнения (4.5) находим составляющую :

= (49∙25 - 5035∙42 + (447,6 + 1030) ∙ 200)/60 = 1421 Н.

5. Векторное уравнение для диады 2–3 с двумя искомыми векторамии, известными по направлению, следует записывать по трём правилам.

Правило 6. При составлении векторного уравнения вначале записывают векторы, известные по величине и направлению; векторы, известные только по направлению, ставят в конец уравнения.

Правило 7.  Последовательно записывают векторы сил, действующих на звенья: вначале на одно звено, затем на другое.

Правило 8. Нормальные и тангенциальные составляющие реакций располагают рядом.

Для выбора масштаба плана сил рекомендуется под уравнением подписать модули сил. В данном примере векторное уравнение:

.                              (4.6)

1738 20 5269 49  5035 1421

В уравнении (4.6) отсутствуют моменты сил; они присутствуют неявно в виде реакций  и, которые определены из формул (4.4) и (4.5), содержащих моменты сил. Масштаб плана сил определяем по наибольшему вектору:

= 37/5269 = 0,007 мм/Н.                             (4.7)

Длины отрезков, изображающих известные векторы:

 = 1738 ∙ 0,007 = 12 мм;    =1421 ∙ 0,007 = 10 мм.          (4.8)                 

 = 20 ∙ 0,007 = 0,14 мм;  = 49 ∙ 0,007 = 0,34 мм;  =  5035 ∙ 0,007 = 35 мм.

Отрезки  и  меньше 2 мм и на плане сил не показываем. План сил диады 2-3 (рис. 4.2) строим по уравнению (4.6). Проводим первый отрезок длиной 12 мм в направлении, противоположном изображённому на рис. 4.1, так как из моментного уравнения получена отрицательная величина . Из его конца проводим отрезок = 37 мм, далее отрезки = 35 мм  и = 10 мм. Из конца отрезка  проводим ему перпендикулярное направление , а из начала - перпендикулярное направление  до его пересечения с направлением .

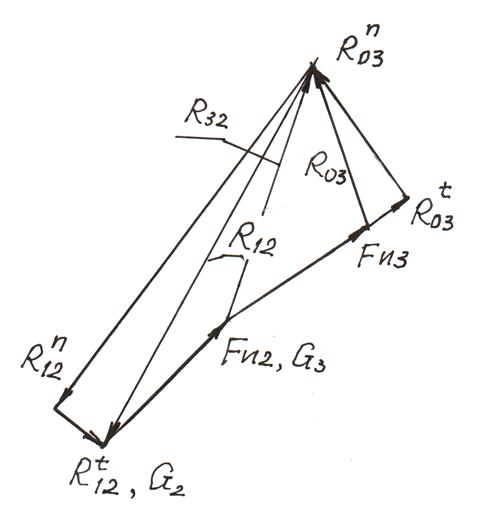
Рис. 4.2

        Векторный многоугольник в соответствии с уравнением (4.6) должен быть замкнутым, так как правая часть уравнения равна нулю. Это означает, что на плане сил стрелки векторов должны следовать друг за другом. Полные реакции определяют геометрическим суммированием в виде векторов, проведенных из начала первого вектора  в конец второго . Из построений находим модули векторов:

= 93/0,007 = 13286 Н;     = 37/0,007 = 5286 Н.

Направления векторов определяют из плана сил (рис. 4.2).