Рассмотрим СП
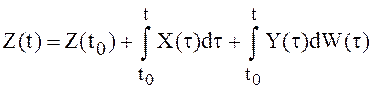 (25)
(25)
где X(t), Y(t)- cлучайные функции и W(t) –
винеровский процесс интенсивности ![]() . Пусть далее
. Пусть далее ![]() - случайная функция , φ(.,.)-
действительная скалярная функция, непрерывная вместе со своими первыми и
вторыми производными по всем компонентам вектора Z и первой
производной по t. Тогда стохастический дифференциал Ито для
случайной функции U(t) будет иметь вид [4]:
- случайная функция , φ(.,.)-
действительная скалярная функция, непрерывная вместе со своими первыми и
вторыми производными по всем компонентам вектора Z и первой
производной по t. Тогда стохастический дифференциал Ито для
случайной функции U(t) будет иметь вид [4]:
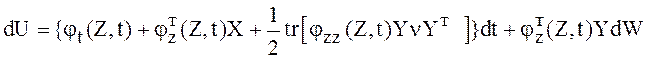 (26)
(26)
Формула (26) называется формулой Ито, от обычного дифференциала сложной функции она отличается последним слагаемым в фигурных скобках.
В формуле приняты обозначения: φ(Z,t.)=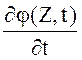 ,
, 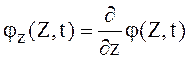 -
матрица- столбец, элементами которой служат производные функции φ(Z,t) по
компонентам вектора Z, а
-
матрица- столбец, элементами которой служат производные функции φ(Z,t) по
компонентам вектора Z, а 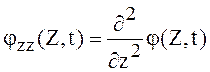 - матрица вторых
производных
- матрица вторых
производных ![]() по компонентам вектора Z.
по компонентам вектора Z.
Пример 15. Пусть:
![]() . Вычислить дифференциал Ито случайной функции.
. Вычислить дифференциал Ито случайной функции.
Решение. Согласно формуле (26)
![]() ,
(27)
,
(27)
так
как в этом случае X(t)=0, Y(t)=1, Z(t)=W(t) и ![]() .
.
Пример 16. Проинтегрируем
полученную формулу (27) по отрезку [0,Т], помня, что W(0)=0 (иначе
говоря от дифференциальной формы записи полученного результата (27) перейдем к
интегральной): 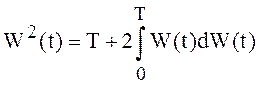 , откуда
, откуда
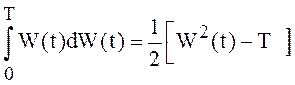 (28).
(28).
Видим, что интеграл Ито от стандартного винеровского процесса по этому же процессу нельзя вычислять по обычной формуле интегрирования степенной функции.
Стохастический
![]() - интеграл при любом
- интеграл при любом ![]() отличается от интеграла Ито на величину
отличается от интеграла Ито на величину ![]() Т ( и не только для частного случая такого
интеграла (28), но и для интегралов общего вида
Т ( и не только для частного случая такого
интеграла (28), но и для интегралов общего вида 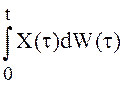 ):
):
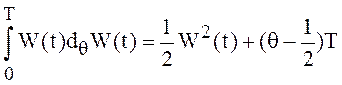 (29)
(29)
В частности, 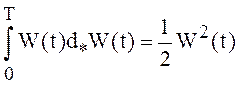 -
для интеграла Стратоновича,
-
для интеграла Стратоновича, 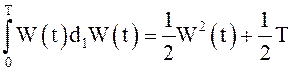 - для интеграла
- для интеграла ![]() .
.
Видим, что значения стохастических θ –интегралов существенно отличаются друг от друга при различных значениях θ, особенно, если Т достаточно велико.
Пример 17. Пусть
![]() . Вычислить дифференциал Ито.
. Вычислить дифференциал Ито.
Решение. 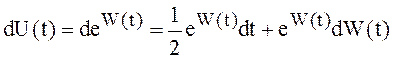 .
.
Введенное понятие стохастического интеграла Ито позволяет рассмотреть класс дифференциальных уравнений со случайной правой частью.
Пусть ![]() - матричная функция
размерности
- матричная функция
размерности ![]() ,
, ![]() -
- ![]() -мерный стандартный винеровский процесс и
-мерный стандартный винеровский процесс и ![]() - вектор начальных условий.
- вектор начальных условий.
Определение 15. СФ X(t) является решением стохастического дифференциального уравнения
![]() (30)
(30)
на
отрезке ![]() с начальным условием
с начальным условием ![]() , если для
каждого
, если для
каждого ![]() ее можно представить в виде
ее можно представить в виде
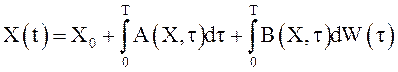 ,
(31)
,
(31)
где в формуле (31) первый интеграл в правой части понимается в с.к. смысле, а второй – является интегралом Ито (см. также формулы 23 и 24).
От дифференциальных уравнений п. 3.5.1 уравнения (30) отличаются наличием в них дифференциала Ито. Решение уравнения (30) подобно решению уравнения (8) из п. 3.5.1.
В главе VП мы будем говорить о стохастических дифференциальных уравнениях этого типа, а сейчас рассмотрим примеры.
Пример 18. Показать,
что СФ ![]() удовлетворяет стохастическому
дифференциальному уравнению
удовлетворяет стохастическому
дифференциальному уравнению 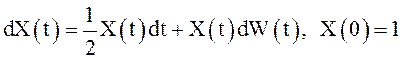 .
.
Решение.
Рассмотрим ![]() в виде
в виде ![]() , где
, где ![]() . Используем результаты примера 16:
. Используем результаты примера 16: 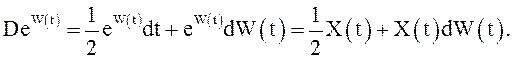 Кроме того,
Кроме того, ![]() .
Следовательно,
.
Следовательно, ![]() действительно является решением
уравнения.
действительно является решением
уравнения.
Пример 19. Пусть
X(t) удовлетворяет линейному дифференциальному стохастическому уравнению ![]() с непрерывными коэффициентами A, G.
Показать, что процесс
с непрерывными коэффициентами A, G.
Показать, что процесс
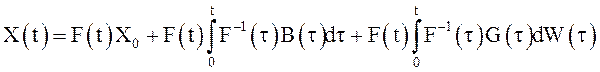 (32)
(32)
является решением этого дифференциального уравнения, если матричная функция F(t) удовлетворяет системе дифференциальных уравнений
![]() (33)
(33)
Решение. Вычислим дифференциалы слагаемых в правой части равенства (32) , используя правило с.к. дифференцирования и формулу Ито:
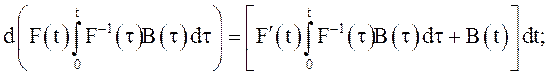
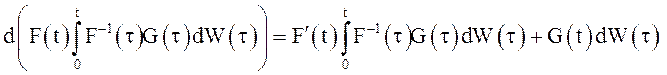 .
.
В последнем равенстве учтено, что для 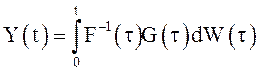 по
определению справедливо
по
определению справедливо ![]() , а по правилу Ито в
силу линейности преобразования
, а по правилу Ито в
силу линейности преобразования ![]() имеет место
имеет место ![]() Окончательно получаем
Окончательно получаем 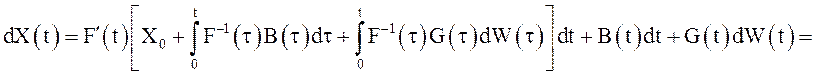 =
=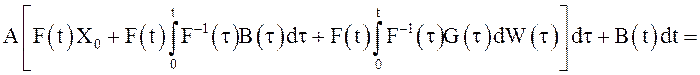
=![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.