Определение 8.
Последовательность случайных функций ![]() ,
, ![]() , называется слабо с.к. сходящейся (с.с.к.
сходящейся) к случайной функции X(t) (по отношению к
, называется слабо с.к. сходящейся (с.с.к.
сходящейся) к случайной функции X(t) (по отношению к ![]() ), если
), если 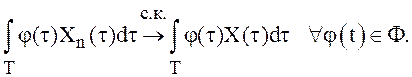
Случайная функция X(t)
называется в этом случае слабым средним квадратическим пределом (с.с.к.
пределом) последовательности ![]() .
.
Класс функций ![]() обычно
в определении не указывается, так как он естественно определяется условиями
задачи. Обычно это класс непрерывных функций, или непрерывных со своими
производными до определенного порядка, или бесконечно дифференцируемых функций.
обычно
в определении не указывается, так как он естественно определяется условиями
задачи. Обычно это класс непрерывных функций, или непрерывных со своими
производными до определенного порядка, или бесконечно дифференцируемых функций.
Пример 11.
Пусть ![]() ,
,![]() , таковы, что
, таковы, что ![]() ,
,
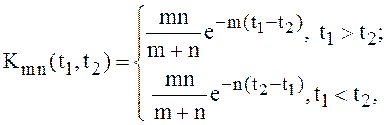 ;
; ![]() при
при ![]() , если
, если ![]() ,
, ![]() при
при ![]() , если
, если ![]() . Далее,
. Далее,
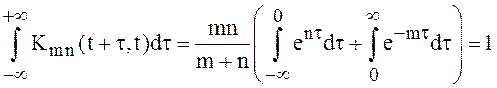
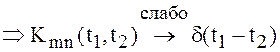 при
при ![]() . Поэтому естественно считать с.к. пределом
. Поэтому естественно считать с.к. пределом
![]() белый шум единичной интенсивности. Но, как
показывают первые два равенства, последовательность не имеет с.к. предела в
точках
белый шум единичной интенсивности. Но, как
показывают первые два равенства, последовательность не имеет с.к. предела в
точках ![]() , следовательно, вообще не имеет с.к.
предела.
, следовательно, вообще не имеет с.к.
предела.
Рассмотрим ![]() , где
, где ![]() - любая непрерывная финитная функция .
- любая непрерывная финитная функция .
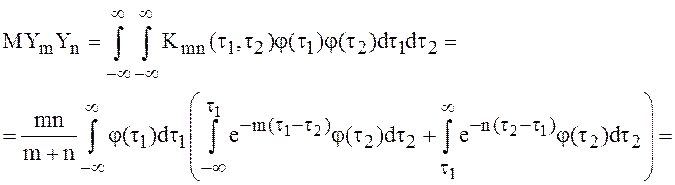
Приведенный пример показывает, что в общем случае с.с.к. предел последовательности случайных функций может не быть случайной функцией в обычном смысле. Это вызывает необходимость расширить понятие случайной функции.
Определение 9. Слабый средний квадратический предел последовательности случайных функций называется обобщенной случайной функцией.
Белый шум относится к классу случайных обобщенных функций.
Очевидно, что из с.к. сходимости с.с.к. сходимость следует: любая с.к. сходящаяся последовательность случайных функций с.с.к. сходится к той же предельной функции. Следовательно, класс обобщенных случайных функций содержит и некоторые обычные случайные функции.
Определение 10.
Пусть V(t)- с.с.к. предел последовательности с.к.
интегрируемых функций ![]() . Интегралом от белого шума
. Интегралом от белого шума ![]() называется с.к. предел интегралов от
случайных функций
называется с.к. предел интегралов от
случайных функций ![]()
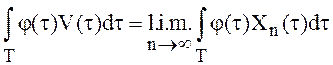 (12)
(12)
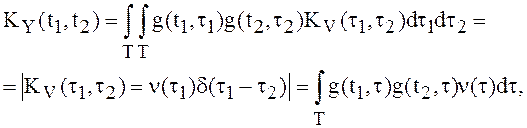 (13)
(13)
где
ν(τ) – интенсивность белого шума, ![]()
При решении практических задач большое значение имеет
вопрос: можно ли по одной реализации СП делать выводы о свойствах СП.
Оказывается, что в некоторых случаях это возможно. Для стационарных СП, кроме
средних статистических характеристик, вводятся еще характеристики, средние по времени.
Пусть ![]() ая реализация СП X(t),
ая реализация СП X(t), ![]() .
.
Рассмотрим 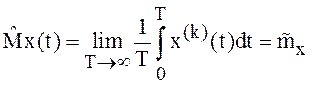 . Здесь символом
. Здесь символом ![]() обозначено усреднение по времени.
Аналогично можно ввести временную функцию корреляции
обозначено усреднение по времени.
Аналогично можно ввести временную функцию корреляции
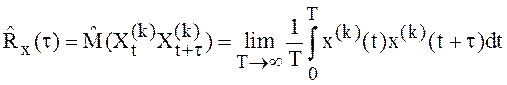 .
.
Следует отметить, что не для всех процессов временные
средние ![]() и
и ![]() имеют
конечные значения. Это во-первых. Если они и имеют конечные значения , то они
могут меняться от реализации к реализации. Это во- вторых. Процессы, для
которых временные средние конечны и одинаковы для всех реализаций, и, кроме
того, совпадают с соответствующими статистическими средними, носят название
эргодических процессов.
имеют
конечные значения. Это во-первых. Если они и имеют конечные значения , то они
могут меняться от реализации к реализации. Это во- вторых. Процессы, для
которых временные средние конечны и одинаковы для всех реализаций, и, кроме
того, совпадают с соответствующими статистическими средними, носят название
эргодических процессов.
В эргодических процессах статистические средние с вероятностью , сколь угодно близкой к 1, равны временному среднему, полученному усреднением одной единственной реализации за достаточно большой промежуток времени. По одной реализации СП можно сделать выводы о свойствах СП.
Определение 10 . Скалярный СП X(t), ![]() , с.к. интегрируемый на
Т с весом
, с.к. интегрируемый на
Т с весом 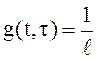 , имеющий постоянное математическое
ожидание
, имеющий постоянное математическое
ожидание ![]() , называется эргодическим по
отношению к МО
, называется эргодическим по
отношению к МО ![]() , если существует
, если существует 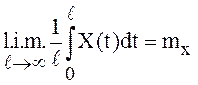 или, что то же самое, cуществует
или, что то же самое, cуществует
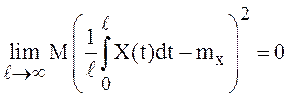 .
.
Теорема 7. Пусть
X(t), ![]() , - скалярный СП с
конечным моментом второго порядка, интегрируемый на множестве T с
весом
, - скалярный СП с
конечным моментом второго порядка, интегрируемый на множестве T с
весом ![]() , где
, где ![]() -
некоторая неслучайная функция, интегрируемая на T. Предел в
среднем квадратическом смысле
-
некоторая неслучайная функция, интегрируемая на T. Предел в
среднем квадратическом смысле 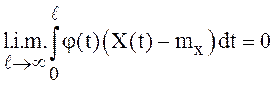
существует тогда и только тогда, когда существует предел
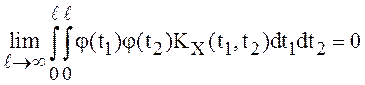 .
.
Доказательство. По условию существует случайная величина
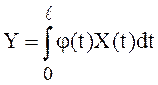 , с
, с 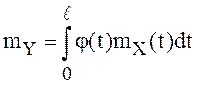 ,
, 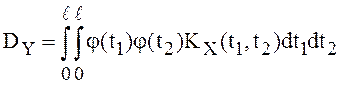 .
.
С другой стороны, 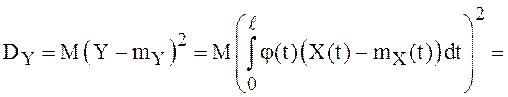
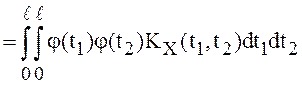 . Предел
левой части при
. Предел
левой части при ![]() равен нулю тогда и только тогда,
когда равен нулю предел правой части при
равен нулю тогда и только тогда,
когда равен нулю предел правой части при ![]() .
.
Следствие 1.
Если в роли φ(t) в теореме взять 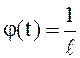 ,
, ![]() , то
, то
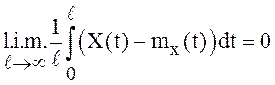 тогда и только тогда, когда
тогда и только тогда, когда 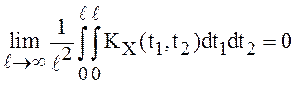 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.