Операции анализа над случайными функциями, страница 6

Следствие 2.  Если 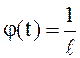, , то условие существования предела 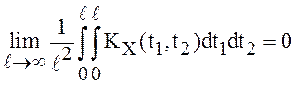   является необходимым и достаточным условием  для эргодичности СП X(t) , , по отношению к его математическому ожиданию.

В вычислительном отношении  иногда гораздо проще  использовать следующее достаточное условие эргодичности СП:

Теорема 8.  Для эргодичности СП X(t), , по отношению к его математическому ожиданию , с.к. интегрируемого на T с весом , достаточно существования предела .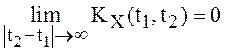

Пример 12.  Пусть X(t), , - стационарный скалярный СП  с

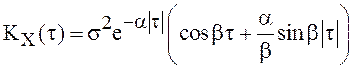,  , . Является ли процесс эргодическим?

Решение. Процесс является эргодическим по отношению к его математическому ожиданию, так как

1) его математическое ожидание  - является постоянным;

2) процесс является с.к. интегрируемым на любом отрезке  с весом , поскольку существуют интегралы 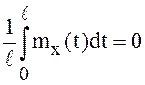    и ;

3) выполняется достаточное условие теоремы 8, которое при  означает существование предела .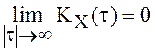

Эргодичность скалярного СП X(t), , относительно его математического ожидания означает, что если известна его реализация x(t), то в качестве оценки  может быть взята величина , то есть 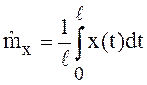. Чем больше величина , тем точнее оценка.

3.8. Стохастический интеграл от  неслучайной функции

Пусть - неслучайная функция,  X(t),  – скалярный СП с некоррелированными приращениями, 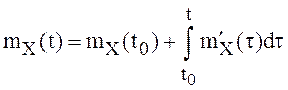,  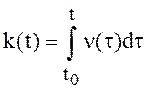, где  и  -также непрерывные функции,  - интенсивность процесса X(t) . Для произвольных разбиений отрезка  точками 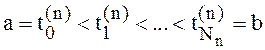 с мелкостями разбиений 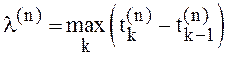, , составим интегральные суммы 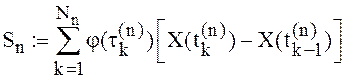,  - произвольные точки отрезка 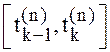 при числе разбиений .

Определение 11 .Стохастическим интегралом от функции  по процессу X(t) называется с.к. предел последовательности  при , если он существует и не зависит ни от разбиения отрезка , ни от выбора точек :

.

Теорема 9. Для существования стохастического интеграла от неслучайной функции  по процессу с некоррелированными приращениями необходимо и достаточно существование пределов: 

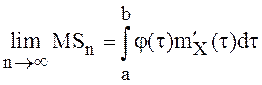 и .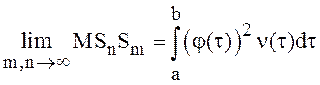       

При этом в силу результатов п. 3.1  м.о. и ковариационная матрица (дисперсия в случае скалярного СП) стохастического интеграла определяются формулами:

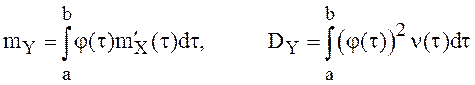                                       (14)

Пример 12.  Найти м.о. и дисперсию стохастического интеграла 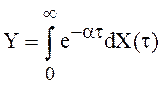, если X(t) – стандартный винеровский процесс, .

Решение. Для винеровского процесса  и , ковариационная функция имеет вид 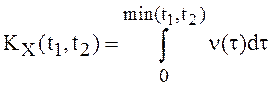     =min(). Тогда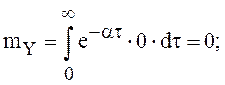       

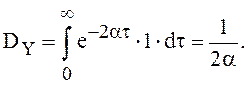
Пример 13.  Найти м.о.  и дисперсию стохастического интеграла 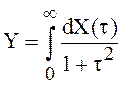, если X(t) – пуассоновский процесс постоянной интенсивности .

Решение. Пуассоновский процесс есть процесс с независимыми приращениями c  конечными моментами второго  порядка, следовательно, он является СПНРП, поэтому задание интеграла по пуассоновскому процессу корректно.

Известно, ,    тогда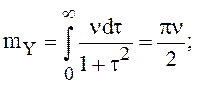      

      

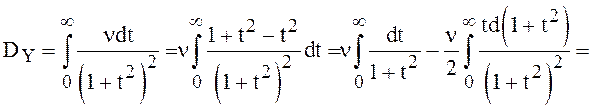
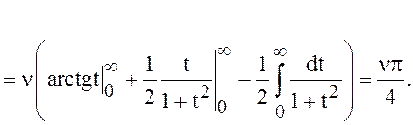
Замечания.  1. Если в определении    стохастического интеграла  СП X(t) – векторный, то , - матрицы, вторая формула (14) принимает вид 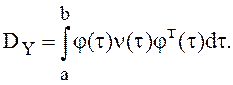 Необходимым и достаточным условием существования векторного стохастического интеграла является существование всех скалярных интегралов, входящих в его состав.

2. Если  и X(t) – СПНРП, тогда справедлива формула интегрирования по частям:

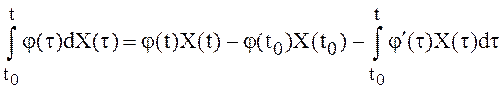             (15)         

Формула (15) выражает стохастический интеграл через с.к. интеграл и это равенство может быть принято за определение стохастического интеграла.

3.9.  Стохастические интегралы как интегралы, содержащие белый шум

Покажем, прежде всего, что СПНРП не являются с.к. дифференцируемыми процессами. Пусть X(t) – СПНРП и

,    .

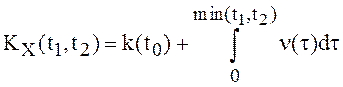Для с.к. дифференцируемости СП X(t) необходимо и достаточно существование конечной второй производной 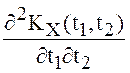. Рассмотрим сначала  как функцию  при фиксированном , тогда 

.

Дифференцируя эту формулу по , находим

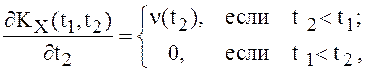
откуда следует, что функция 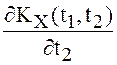 в точке    терпит разрыв  с величиной скачка, равной . Последнее равенство можно записать в ви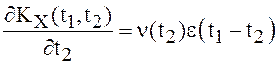де , где  - единичная функция. Продифференцируем последнее равенство по , получим

.                 (16)

При  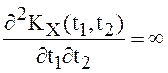 , следовательно условие с.к. дифференцируемости процесса не выполнено.