Операции анализа над случайными функциями, страница 7

Однако выражение для второй производной ковариационной функции содержит множителем -функцию, но тогда это ковариационная функция белого шума. Поэтому целесообразно считать с.к. производную СПНРП X(t) белым шумом. Для формального же доказательства этого факта достаточно показать, что любой СПНРП имеет слабую с.к. производную, представляющую собой белый шум той же интенсивности, что и СПНРП.

На основании вышеизложенного стохастический интеграл можно формально представить в виде интеграла, содержащего белый шум:

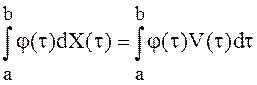                                         (17)

Если в интегралах заменить a на  , b – на t и  на , то они примут вид:

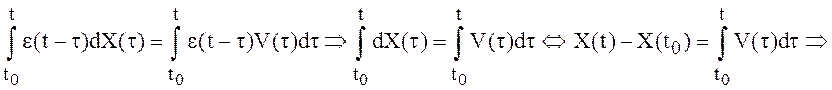
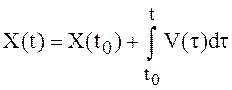                                                     (18)

Последний результат означает, что любой с.к. непрерывный процесс с некоррелированными приращениями можно представить в виде интеграла от белого шума той же интенсивности.

3.10. Стохастический интеграл по ортогональной стохастической мере

Отметим, что введенный выше стохастический интеграл от неслучайной функции представляет собой частный случай стохастических интегралов от неслучайных функций по ортогональной стохастической мере. Приведем коротко некоторые определения.

Пусть задано вероятностное пространство  и некоторое множество  с σ – алгеброй ε его подмножеств.

Определение 12. Функция (может быть и комплексная)  называется элементарной стохастической мерой , если выполнены условия: 1)  - центрированная случайная функция с конечным вторым моментом, то есть  2) для любых  3) если - последовательность  из  ε такая, ч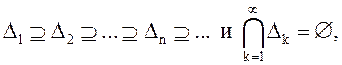то  то .

Если дополнительно выполняется условие , что   то есть  ортогональна , то стохастическая  мера называется ортогональной.

С каждой стохастической мерой  связана неслучайная мера  определенная следующим образом:  Она называется структурной функцией стохастической меры. С каждой же конечной мерой связана функция распределения - это любая функция  обладающая свойствами: 1)  - неубывающая функция,  2)  если  и  3)  - непрерывная справа функция. Говорят еще, что неслучайная конечная мера порождает функцию распределения. С помощью функции распределения  мера  на каждом промежутке  задается следующим образом:

.

Определение стохастического интеграла по ортогональной стохастической мере от неслучайной функции полностью повторяет определение интеграла Лебега. Пусть f(x) – некоторая простая функция на Е, то есть  такая, что 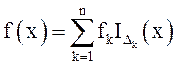 и  - индикаторная функция  множества . Стохастическим интегралом по ортогональной мере   от простой функции f(x) называется с. величина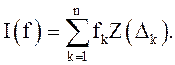

Если  аппроксимируется последовательностью простых функций  и  простые функции на Е, то        с. в.  называется стохастическим интегралом на Е от произвольной неслучайной функции по ортогональной стохастической мере.

Перечислим некоторые свойства стохастических интегралов.

1.

2. числа;

3.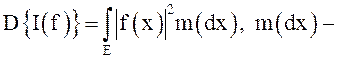структурная функция меры  на ε.

4. .

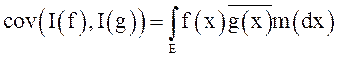Далее, из теории стохастических мер известно, что стохастическая ортогональная мера  на борелевской σ – алгебре ε подмножеств  отрезка  может быть задана с помощью центрированных с. к. непрерывных СП X(t),  с некоррелированными приращениями, , иначе говоря, с помощью процессов с ортогональными приращениями (см.п. 2.2). В этом состоит еще одна особенность СП с ортогональными приращениями.   Если , то случайная функция  обладает всеми свойствами элементарной ортогональной стохастической меры на ε . Структурная функция   этой ортогональной стохастической меры  имеет вид:  - см. формулу (6) гл. П. По определению дисперсии процесса с некоррелированными приращениями его дисперсия является функцией неубывающей, непрерывной в силу с. к. непрерывности СП X(t), а также равной нулю при t=0, так как    . Можно полагать поэтому, что  является функцией распределения  меры .

Интегралы по стохастической ортогональной мере, порожденной СП  X(t) с ортогональными приращениями, записывают обычно в следующем  виде: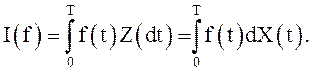    

Поскольку часто в роли таких процессов выступают винеровские процессы, то последняя запись преобразуется к виду 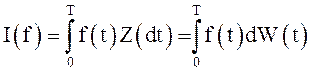 ( см. следующий параграф).