Если X(t) дифференцируема в каждой точке ![]() , то семейство случайных величин
, то семейство случайных величин ![]() называется с.к. производной процесса X(t) на
Т.
называется с.к. производной процесса X(t) на
Т.
Теорема 3.
Случайная функция X(t) с.к. дифференцируема в области Т тогда и только
тогда, когда существует конечная производная 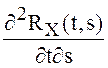 во
всех точках
во
всех точках ![]() .
.
Доказательство.
По стохастическому критерию Коши с.к. предел 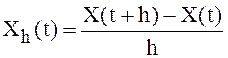 при
при ![]() существует тогда и только тогда, когда
существует конечный предел момента
существует тогда и только тогда, когда
существует конечный предел момента
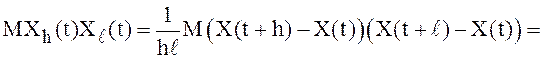
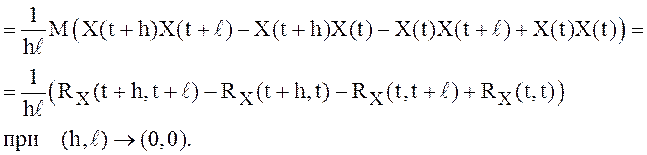
Но если этот предел существует, то он равен второй
смешанной производной 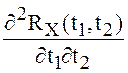 в точке
в точке ![]() . Тогда по свойствам ковариационной
функции, если эта производная существует на точках диагонали квадрата Т
. Тогда по свойствам ковариационной
функции, если эта производная существует на точках диагонали квадрата Т![]() Т, то она существует и всюду в квадрате
Т
Т, то она существует и всюду в квадрате
Т![]() Т.
Т.
В условиях теоремы 3 во всех точках ![]() существуют производные
существуют производные 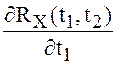 ,
, 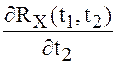 и
справедливы формулы
и
справедливы формулы
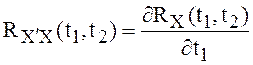 ,
, 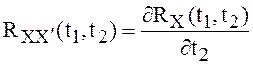 . (1)
. (1)
Действительно, 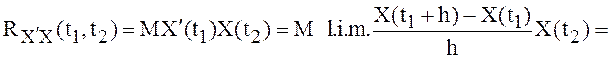
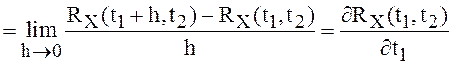 .
.
В вычислениях воспользовались замечанием в конце п.3.1
Из второй формулировки стохастического критерия Коши следует утверждение:
Теорема 4. Cлучайная функция X(t) с.к. дифференцируема в области Т тогда и только тогда, когда существуют
1) конечная производная функции ![]() во всех точках
во всех точках ![]() и
и
2) конечная вторая смешанная производная ее
ковариационной функции ![]() во всех точках
во всех точках ![]() .
.
Справедливы формулы:
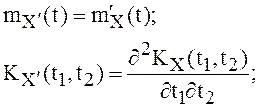
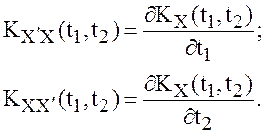 (2)
(2)
Обычным образом определение с.к. производной обобщается на случай с.к. производной СФ X(t) более чем первого порядка.
Из теоремы о с.к. сходимости для конечномерных векторных СФ следует, что векторная СФ X(t) с.к. дифференцируема на Т тогда и только тогда, когда выполнено одно из следующих двух равноценных условий:
1)
существует конечная производная 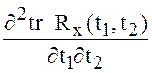 во всех точках
во всех точках![]() ;
;
2)
математическое ожидание ![]() дифференцируемо на Т и существует конечная
производная
дифференцируемо на Т и существует конечная
производная 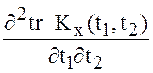 во всех точках
во всех точках ![]() .При этом всюду на
.При этом всюду на ![]() существуют
производные
существуют
производные 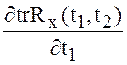 ,
, 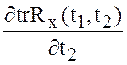 ,
, 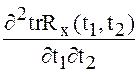 ,
, 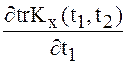 ,
, 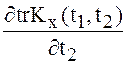 ,
, 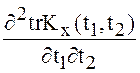 и
справедливы формулы (1), (2).
и
справедливы формулы (1), (2).
Замечание.
Если X(t), ![]() , стационарный процесс,
то
, стационарный процесс,
то ![]() .
.
Если существует процесс ![]() , то для
него
, то для
него
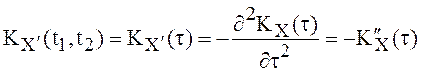 ,
, ![]() , и
, и ![]() .
.
Пример 4.
Пусть центрированная СФ X(t) имеет ковариационную функцию ![]() Вычислить
дисперсию ее с.к. производной.
Вычислить
дисперсию ее с.к. производной.
Решение.
Поскольку ![]() то остается проверить на
дифференцируемость ковариационную функцию
то остается проверить на
дифференцируемость ковариационную функцию ![]() - она
бесконечно дифференцируема. Тогда
- она
бесконечно дифференцируема. Тогда 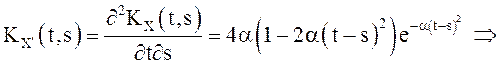
![]()
Отметим, что операция с.к. дифференцирования является
линейной операцией. Пусть 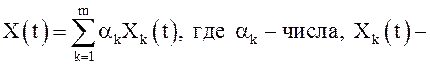 с.к. дифференцируемые
случайные функции. Тогда
с.к. дифференцируемые
случайные функции. Тогда 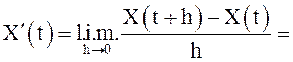
=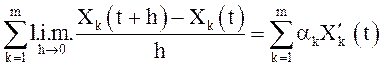 . Иными словами, с.к. производная линейной
комбинации с.к. дифференцируемых функций является линейной комбинацией их с.к.
производных, что и означает линейность операции с.к. дифференцирования.
. Иными словами, с.к. производная линейной
комбинации с.к. дифференцируемых функций является линейной комбинацией их с.к.
производных, что и означает линейность операции с.к. дифференцирования.
Этот результат можно обобщить в следующем направлении:
если неслучайная функция ![]() дифференцируема на Т, а
СФ X(t) – с.к. дифференцируема на Т, то СФ
дифференцируема на Т, а
СФ X(t) – с.к. дифференцируема на Т, то СФ ![]() имеет
с.к. производную
имеет
с.к. производную ![]()
Однако не следует думать, что все СФ с.к. дифференцируемы.
Пример 5. Рассмотрим
винеровский процесс W(t), ![]() ,
, ![]() , и решим вопрос об его с.к.
дифференцируемости. Пусть
, и решим вопрос об его с.к.
дифференцируемости. Пусть ![]() .
.
При
![]() величина
величина 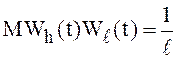 не
имеет конечного предела. Это означает, что винеровский процесс не является
с.к. дифференцируемым ни при каком
не
имеет конечного предела. Это означает, что винеровский процесс не является
с.к. дифференцируемым ни при каком ![]() :
: 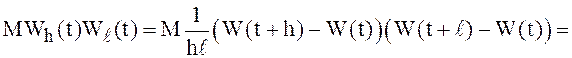
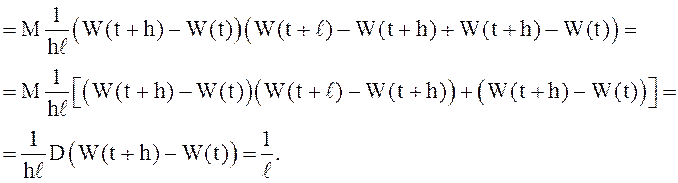
Сделаем еще одно важное замечание.
Дифференцируемость случайных функций весьма легко проверяется, сравнительно
легко вычисляются вероятностные характеристики производных случайных функций.
К сожалению, явный вид процесса ![]() по приведенным выше
теоремам получить не удается. Это удается сделать в некоторых случаях на основе
следующего определения.
по приведенным выше
теоремам получить не удается. Это удается сделать в некоторых случаях на основе
следующего определения.
Определение 5.
Случайная функция X(t), ![]() , называется
дифференцируемой на Т (потраекторно), если почти все ее траектории –
дифференцируемые функции, то есть
, называется
дифференцируемой на Т (потраекторно), если почти все ее траектории –
дифференцируемые функции, то есть ![]() .
.
Покажем, как использовать определение для получения
процесса ![]() . Пусть
. Пусть ![]() -
производная траектории СП X(t),
-
производная траектории СП X(t), ![]() - с.к. производная X(t),
- с.к. производная X(t), ![]() , то
, то 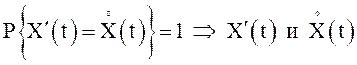 -
стохастически эквивалентны, то есть
-
стохастически эквивалентны, то есть ![]() .
.
Пример 6.
Пусть 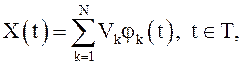 где
где ![]() -
некоррелированные случайные величины с математическими ожиданиями
-
некоррелированные случайные величины с математическими ожиданиями ![]() дисперсиями
дисперсиями ![]() а
а ![]() - непрерывные на Т неслучайные функции.
Найти
- непрерывные на Т неслучайные функции.
Найти ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.